機械設計者の基礎知識4力学に触れよう。 第2回 加速トルクの計算
本連載では、技術士の春山先生に、設計者の方へ向け材料力学・機械力学・熱力学・流体力学の「4力」について解説いただいています。実務で使用できる例題をご用意しているため、日々の業務に取り入れやすい内容です。
第二回は機械力学についてです。
【加速トルクの計算】
はじめに
機械設計を行う際、いくつかの機械要素を選定することがあります。この機械要素を選定するにあたっては、いくつかの力学の知識が必要となることがあります。
例えばモーターを使って何か物体を回そうとしたときに、必要な加速トルクを計算するためには回転の対象の慣性モーメントを計算する必要があります。
これは機械力学の知識に当たります。
本来、機械設計を行う者には基礎的な力学知識が必要なのです。
［１］ボールねじを使った搬送テーブルの加速トルクを計算してみよう。
モーターのトルク計算はその使い方、例えばワークを巻き上げるのか？ベルトコンベヤのようなものを駆動させるのか？ボールねじなどを使って直線運動させるのか？などによって計算式が多少異なります。詳細はメーカーのHPやカタログなどに記載があるのでそちらを参照していただくとして、ここではボールねじを使ってワークを直線運動させる場合を代表例として取り上げます。
［問題］
ボールねじを使った水平搬送に必要なトルクの計算
図2に示すようにモーター軸をカップリングを介してボールねじに繋ぎます。ボールねじの両サイドには直動ガイドがあり、ボールねじを回転させることでワークを載せた搬送テーブルが水平移動します。ワークを含めた水平搬送部の質量mは20kgとします。搬送のトップスピードは0.2m/s、停止～トップスピードまでの加速時間は0.2sとします。
設計初期段階で選定した機械要素のスペックは次の通りになりました。
(1)ボールねじのスペック
・リード 5㎜
・軸外径 15㎜
・ねじ長さ 750㎜
(2)モーターのスペック
・定格出力 50W
・定格トルク 0.159N・m
・回転子慣性モーメント
0.0665×10-4kg・m2
(3)カップリングのスペック
・許容トルク 1N・m
・慣性モーメント
0.021×10-4kg・m2
＊直動ガイドによるロスは今回は考慮せず、あくまで回転体に着目します。
以上のような条件のとき、モータートルクは十分足りているでしょうか？
⇩
［ポイント］
加速トルクの計算式
Ta［N・m］=J［kg・m2］×α[rad/s2]
［解答］
加速トルクTaはポイントで示した通り、次式で与えられます。
J：慣性モーメント（kg・m2）
α：角加速度（rad/ s2）
＊慣性モーメントのことをイナーシャIと表現することもありますが、正確には慣性モーメント≠イナーシャです。詳しくは次項で解説します。
ここで問題の系の場合の慣性モーメントは、次のそれぞれの要素の慣性モーメントを求めてそれらを足し合わせたものとなります。
(1)水平搬送部の慣性モーメント
ワークや搬送テーブル、あるいはそれらの付属部品など、水平移動する部品全ての重量から求める慣性モーメントになります。
(2)ボールねじの慣性モーメント
ボールねじのカタログに記載がある場合もありますが、ない場合はボールねじを円筒物体として算出します。
(3)カップリングの慣性モーメント
カップリングのカタログに記載がある場合もありますが、ない場合はカップリングを円筒物体として算出します。
今回の場合、スペックにカップリングの慣性モーメントの記載があるためこれを利用します。
(4)モーター回転子の慣性モーメント
モーターカタログに記載があります。
(3)、(4)はスペックに記載があるので、(1)と(2)を算出していきます。
(1)水平搬送部の慣性モーメントJh
P：ねじリード 5×10-3［m］
(2)ボールねじの慣性モーメントJb
ボールねじをφ15、長さ750の円筒状の物体と考えます。
まずはボールねじの質量mbを求めます。材質は鉄系、密度を7.85×103kg/m3 とします。
よって慣性モーメントは次の通りです。
(3)カップリングの慣性モーメントJc
スペックからJc =0.021×10-4kg・m
(4)モーターの慣性モーメントJm
スペックからJm=0.0665×10-4kg・m2
以上から、この系全体の慣性モーメントJa
この慣性モーメントJaを用いて加速トルクTaを求めます。
ここで、αは角加速度[rad/s2]であり、回転数N[rpm]との関係は角速度ω[rad/s]と加速時間ta[s]を用いて次の通りになります。
よって加速トルクは次式のように変形されます。
さてここで、加速時間taは0.2、トップスピードは0.2m/sと与えられています。これらから回転数N[rpm]を算出します。
・トップスピード 0.2m/s
・ねじリード 5mm
∴トップスピード時の回転数Nは
となります。よって加速トルクは次の通りです。
これを仮で選定したモーターの定格トルクやカップリングの許容トルクと比較して、それらのトルクを超えてしまっている場合は再度選定し直しになります。今回の場合の各許容トルクは以下の通りであり、他のロスを考慮しなくてよいならば特に問題ありません。
モーター定格トルク 0.159N・m
カップリング許容トルク 1N・m
よって特に問題はありません。
[2]慣性モーメント／イナーシャ／はずみ車効果の違いについて
以上で見たようにモーター選定に当たり慣性モーメントは非常に重要なパラメータになります。また、先に述べたようにモーターの使い方によるトルク計算方法はメーカーサイトやカタログを見れば書いてあります。しかしいざ調べてみようとすると、3つの指標が出てきます。それば「慣性モーメント」「イナーシャ」「はずみ車効果」です。
この3者はともに物体の回転しにくさを表しています。しかしそれぞれ厳密には定義が異なります。さらにややこしいことに、単位系の取り方によっては同じ計算結果になったり異なる結果になったりします。
ここでそれぞれの定義について確認しておきます。
(1)慣性モーメントJ
ｍ：質量 [kg]
Ｒ：回転半径 [m]
Ｊ：慣性モーメント[kg・m2]
＊R単純な半径ではありません。例えば図3で見たように半径rを持つ軸を軸回りに回転させる場合の回転半径はR=1/2rとなり、慣性モーメントはJ=1/2mｒ2となります。
(2)イナーシャI
Ｗ：力 [＊1]
ｇ：重力加速度[ｍ/s2]
Ｒ：回転半径 [m]
Ｉ：イナーシャ[＊１]
(3)はずみ車効果GD2（はずみぐるまこうか、ジーディースクウェア）
Ｗ：力 [kgf]
D：回転直径 [m]
GD2：はずみ車効果[kgf・m2]
＊１イナーシャの単位について確認しておきます。
イナーシャの計算には力Wを用います。この力Wの単位に、ニュートンNを用いた場合、W[N]/g[m/s2]=m[kg]となります。つまりイナーシャIは、I=mR2となり、慣性モーメントと同じ値になります。
一方で、力の単位にキログラム重kgfを用いた場合は全く異なる計算結果となるため注意が必要です。2021年現代では、mks単位系が国際単位系として採用されており力の単位は組立単位としてニュートンN（kg・m/s2）が用いられています（１N=9.8×1kgf）。
力の単位にNを採用した場合は、慣性モーメント=イナーシャとなるため、特に区別せずに（混同して）使っているところも多いです。
mks単位系を使用している現代では基本的に慣性モーメント（イナーシャ）を採用します。
[3]慣性モーメントの導出
（円板の慣性モーメントが1/2mr2になる理由の解説です。）
慣性モーメントの定義をここで確認します。
図4に示すように質量mを持つ物体の微小部分の質量をdm、任意の点Oからの距離をrとします。任意の点Oを中心に回転をさせようとしたときの慣性モーメントは次式で与えられます。
なお図5に示すような直交座標系x,y,zの各軸に対する慣性モーメントの関係性は次の通りです。
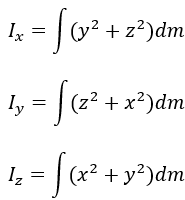
特に厚みが薄い板の場合、板面内にx,y軸を取れば慣性モーメントの関係性は次の通りになります。
ここで図6に示すように質量m、半径Rを持つ円板をz方向（奥行き方向）軸回りに回転させるときの慣性モーメントを考えます。
厚み方向は無視できるものとし、面積密度をρ［kg/m2］とします。中心からrの位置にある微小領域drを考えます。
・・・慣性モーメント定義
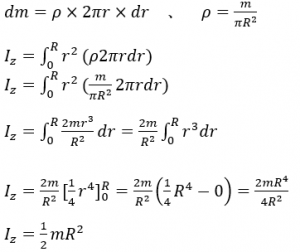
［4］問題
図7に示すように質量m、半径Rを持つ円板をX軸回りに回転させる。このときの慣性モーメントとして正しいものを選べ。
（a）1/2mR2
（b）2/3mR2
（c）1/4mR2
（d）3/4mR2
解答はウェビナーで解説いたします。
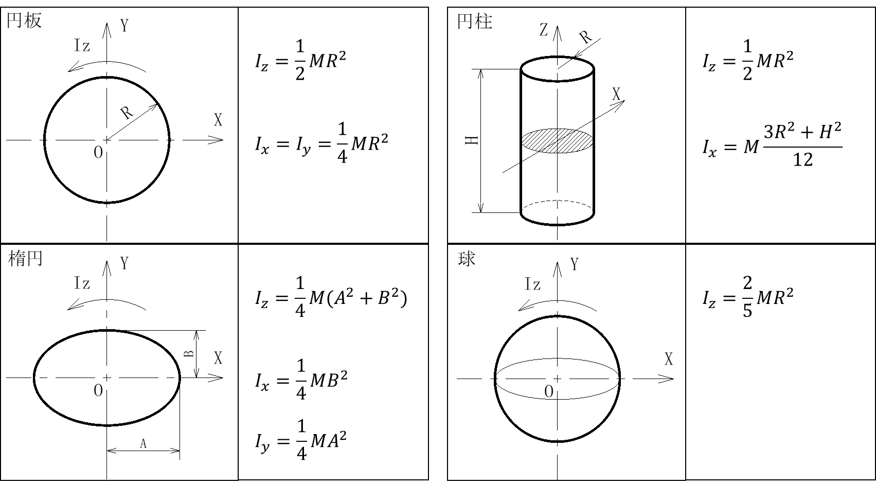
［5］各種形状の慣性モーメント
円板、円柱、楕円、球の4つの慣性モーメントです。
[おまけ]ACモーターとDCモーター
モーターの選定にはトルク計算も大事ですが、モーターの種類を押さえることも大事になってきます。モーターの種類には多くのものがありますが、最も大きな分類としてACモーター/DCモーターがあります。
AC（Alternating Current） ：交流
DC（Direct Current） ：直流
◆ACモーターとDCモーターの決定的な違い
ACモーター：
周波数で回転数が決まる。一般的な4極モーターの場合、電源周波数が60Hzの西日本で使えば1800rpm、電源周波数が50Hzの東日本で使えば1500rpmとなる。
つまりどれだけ負荷が大きくなっても（あるいは小さくなっても）回転数は変わらない。ただし、許容トルクを超える負荷となると回転できない。
ACモーターの回転数Nの計算式
N=120f/P
ｆ：周波数（Hz）
Ｐ：極数
＊実際にはすべりという現象があり回転数は計算式よりも小さくなります。
DCモーター：
負荷によって回転数が変わる。負荷が大きくなればなるほど回転数が小さく、消費電流が大きくなる。
ＡＣモーターとＤＣモーターの動作原理についてはウェビナーで補足解説いたします。
ウェビナーを開催しています！
