機械設計者の基礎知識4力学に触れよう。 第5回 空気消費量の計算
本連載では、技術士の春山先生に、設計者の方へ向け材料力学・機械力学・熱力学・流体力学の「4力」について解説いただいています。実務で使用できる例題をご用意しているため、日々の業務に取り入れやすい内容です。
第五回はエアシリンダーの空気消費量の計算について、例題を用い解説します。
はじめに
自動機械にはエアシリンダーなどの空圧機器が多用されます。空圧機器を動作させるための圧縮空気はコンプレッサなどから供給されます。コンプレッサの供給能力には限界があります。この限界を超えて機械側で空気を消費してしまうと、当然のように機械の動きがおかしくなってしまいます。
エアシリンダーで消費する空気の量を計算するには熱力学の知識が必要です。
本来、機械設計を行う者には基礎的な力学知識が必要なのです。
[1]エアシリンダーの基本
エアシリンダーは圧縮空気を供給したり排気したりすることで動作する機器です。まずはその基本を見ていきたいと思います。
エアシリンダー自体にもいくつかの種類がありますが、ここではロッド付きエアシリンダーについて見ていきます。
ロッド付きエアシリンダーとは圧縮空気の力を利用してロッドが動作する機械です。その駆動方式には単動式と複動式があり、さらに単動式は単動押し出し式と単動引き込み式に分かれます。まずは複動式の動きについて見ていきます。
(1)複動式
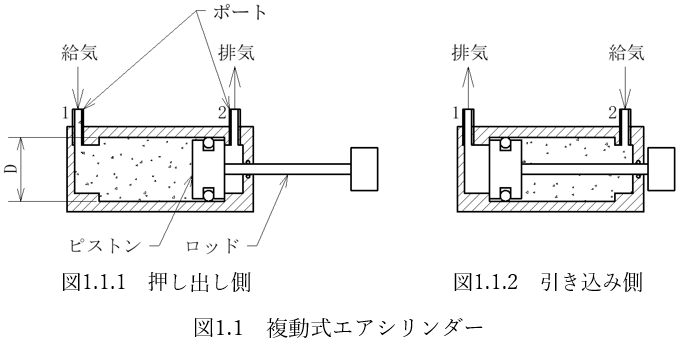
複動式エアシリンダーにはポートと呼ばれる空気の出入り口が2か所あります。図1.1.1に示すように1番ポートを給気、2番ポートを排気するとロッドは押し出されます。
図1.1.2に示すように給気排気を逆転させるとロッドは引き込まれます。まずはこのときの、ロッドの押す力と引く力をそれぞれ確認します。
シリンダーの押す力あるいは引く力は、圧力(P)×受圧面積(A)で求めることができます。図1.1.1に示すようにシリンダーの内径をD、ロッドの外形をd、給気圧力をP、ロッドの押す力をFs、引く力をFlとします。
*以後、押す側に添え字s、引く側に添え字lを付けます。
ピストン・ロッドを押し出すときの受圧面積Asはピストンの面積全面で受けるためAs=πD2/4となります。よってFs=P×πD2/4 で押し出す力を求めることができます。
一方、ロッドを引き込むときの受圧面積Alはロッドの分だけ小さくなります。すなわち受圧面積はAl=π(D2-d2)/4 となり、引き込む力はFl=P×π(D2-d2)/4 となります。
(2)単動式
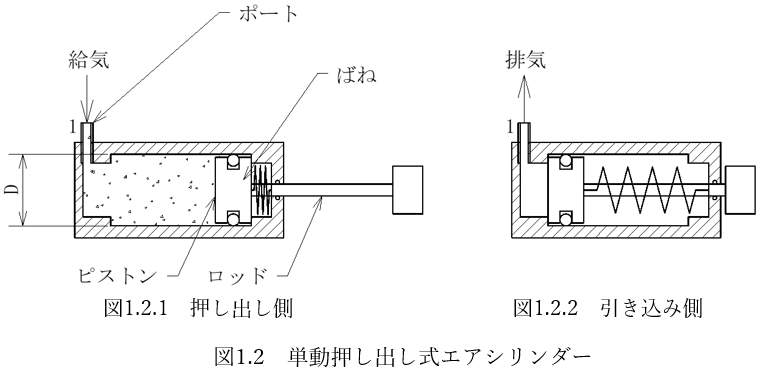
単動式には押し出し式と引き込み式がありますが、単動押し出し式について見ていきます。図1.2に示すように単動式の場合はポートは1つで、内部にばねが組み込まれています。図1.2.1ではポートから給気しています。このときピストン・ロッドはポートからの圧縮空気により押し出されています。図1.2.2に示すようにポート1から排気するとばねの力によってピストン・ロッドは引き込まれます。単動引き込み式の場合はポートとばねの関係が逆になります。
単動式の場合の押す力を見ていきます。“圧縮空気により押し出される力”は複動式と同じでP×πD2/4 となります。
ここで、単動式押し出し式の場合は引き込み用のばねが組み込まれているため、圧縮空気によりピストン・ロッドを押し出したときにはばねの反発力が発生します。このばねによる反発力をFb=kxとすると、単動押し出し式の押す力はFs= P×πD2/4-kx となります。
単動引き込み式の場合はロッドの分、受圧面積が小さくなるためFl=P×π(D2-d2)/4-kx となります。
以上でみたシリンダーの押す力・引く力の計算はあくまで理論値です。実際には機械効率などを考慮する必要があります。またシリンダーの力はメーカーカタログにて一覧表で確認できるので、実際の設計に当たってはカタログを参照してください。
[2]シリンダーの空気消費量
(1)一般式
まずは複動式において、ピストン・ロッドを押し出した状態から引き込んだ状態に変化させたときの空気消費量=排気量について確認していきます。
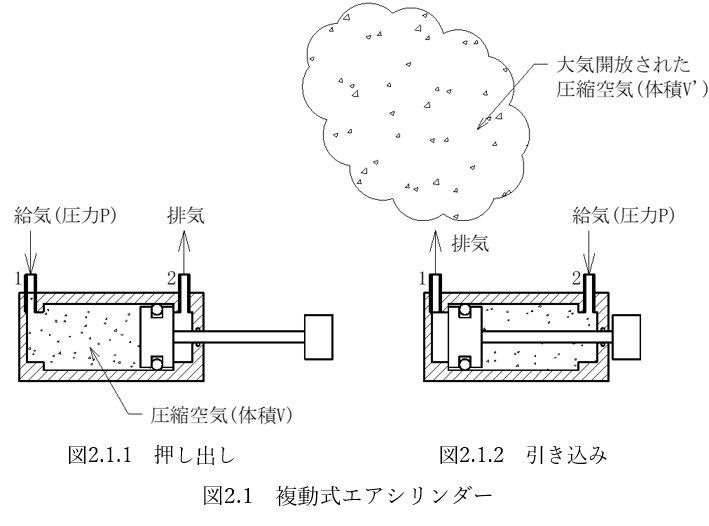
図2.1.1に示すようにポート1に圧力P(ゲージ圧)の圧縮空気を給気、ポート2を排気するとロッドは押し出されます。このときシリンダー内部にはピストン・ロッドの左側に体積Vの圧力P圧縮空気があります。図2.1.2に示すように給気排気を入れ替えることで、圧縮空気は大気に開放(排気)されます。このとき、開放された空気の体積V’が空気の消費量です。
この体積V’はボイル・シャルルの法則から求めることができます。
*ゲージ圧と大気圧についてはウェビナーをご確認ください。
ボイル・シャルルの法則から、気体の体積をV、圧力をP(ゲージ圧)、大気圧をPa、温度をt、気体定数をRとしたときにそれぞれの関係は
(P+Pa)V=Rt
となります。この式を変形すると
R=(P+Pa)V/t
となります。
ここで単位を次のように統一します。
V:体積(L) 、 P:圧力(MPa) 、 S:ストローク(mm) 、 t:温度(摂氏)
*MPa=N/mm2
いまシリンダー内部にある圧縮空気において圧力をP(ゲージ圧)、シリンダー内部の体積をV、温度をtとします。大気圧はPa、シリンダー内部の圧縮空気が大気開放されたときの体積をV’、温度をシリンダー内部の温度と同じでtとします。どちらも空気のため気体定数は同じであり、その値をRとします。
ボイル・シャルルの法則から、開放された圧縮空気の体積V‘は次のようになります。
(P+Pa)V/(273+t)=PaV’/(273+t)
(P+Pa)V=PaV’
V’=(P+Pa)/Pa×V
つまり、エアシリンダーを駆動させたときの空気消費量は圧力Pとシリンダー体積Vから定まります。
シリンダーストロークをSとして複動式、単動押し出し式、単動引き込み式それぞれでの体積Vを確認します。
複動式において
①押し出し状態から引き込み状態への変化の場合、Vl=πD2/4×S×10-6 となります。
②引き込み状態から押し出し状態への変化の場合、はロッド分だけ体積が減ります。
よって、Vs=π(D2-d2)/4×S×10-6 となります。
③複動式を1往復させると空気は①+②消費します。
*単位について補足します。
立法ミリメートルとリットルの関係は1[mm3]=10-6[L]となりす。いま、DやSの単位はmmです。よって
Vl=πD2/4×S[mm3]=πD2/4×S×10-6[L]となります。
単動式において
①単動押し出し式の場合、押し出し状態から引き込み状態への変化のときのみ空気が排気される、つまり消費されます。このときの体積はVl=πD2/4×S×10-6 となります。
②単動引き込み式の場合、引き込み状態から押し出し状態への変化のときのみ空気が排気される、つまり消費されます。このときの体積はVs=π(D2-d2)/4×S×10-6 となります。
押し出したときと引き込んだときとでの空気消費量の計算式を表1にまとめます。また複動式と単動式がそれぞれ1往復したときの空気消費量を表2にまとめます。
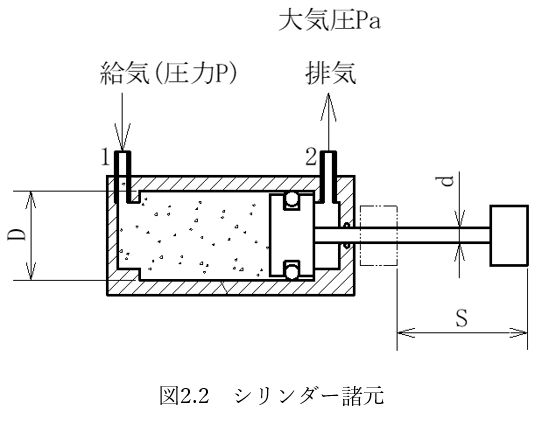
あわせて図2.2にシリンダー諸元を示します。
表1 押し出しのときと引き込みのとき、それぞれにおける空気消費量の計算式
| 押し出し | \[ V_s’=\frac{(P+Pa)}{Pa}× \left[ \frac{π(D^2-d^2)}{4}×S \right] ×\frac{1}{10^6} \] |
| 引き込み | \[ V_l’=\frac{(P+Pa)}{Pa}×\frac{πd^2}{4}×S×\frac{1}{10^6} \] |
表2 複動式と単動式それぞれが1往復したときの空気消費量の計算式
| 複動式 | \[ V_s’= \left[ \frac{(P+Pa)}{Pa}× \left[ \frac{π(D^2-d^2)}{4}×S \right] +\frac{(P+Pa)}{Pa}×\frac{πD^2}{4}×S \right] ×\frac{1}{10^6} \] |
|
| 単動式 | 押し出し | \[ V_s’=\frac{(P+Pa)}{Pa}× \left[ \frac{π(D^2-d^2)}{4}×S \right] ×\frac{1}{10^6} \] |
| 引き込み | \[ V_l’=\frac{(P+Pa)}{Pa}×\frac{πd^2}{4}×S×\frac{1}{10^6} \] |
|
(2)具体的な計算例
問題
シリンダー内径φ63、ロッド外形φ20、ストローク180の複動式エアシリンダーが12秒に1回のサイクルタイムで往復動作します。圧縮空気は元圧0.5MPaで供給されるものをレギュレーターで0.3MPaに絞って供給します。このとき、1分間当たりにエアシリンダーが消費する空気の体積を求めてください。
大気圧は0.1MPaとします。
解答
まずは1往復したときの空気消費量を求めます。複動式の場合は表2から計算式は次式のとおりです。ここに問題で与えられた数字を代入していきます。
\[
V’=
\left[
\frac{(P+Pa)}{Pa}×
\left[
\frac{π(D^2-d^2)}{4}×S
\right]
+\frac{(P+Pa)}{Pa}×\frac{πD^2}{4}×S
\right]
×\frac{1}{10^6}
\]
\[
V’=
\left[
\frac{(0.3+0.1)}{0.1}×
\left[
\frac{π(63^2-20^2)}{4}×S
\right]
+\frac{(0.3+0.1)}{0.1}×\frac{π63^2}{4}×180
\right]
×\frac{1}{10^6}=4.26L
\]
12秒に1回のサイクルタイムということは、1分間で5往復します(60秒÷12秒/回=5回)。よって上で得られた体積に5をかけると求める空気の体積が得られます。
求める体積を添え字1をつけて、V’1とします。
\[
V_1’=4.26×5=21.3L
\]
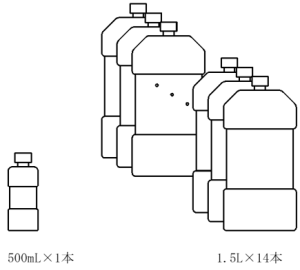
参考までに、内径φ63、ストローク180のシリンダーの体積は約0.56L(560mL)です。おおよそ、500mLのペットボトルと同等の大きさ程度です。このシリンダーに圧力0.3MPaかけて5往復させると21.3L の空気が消費されます。これは1.5Lのペットボトルに換算すると約14本分に相当します。
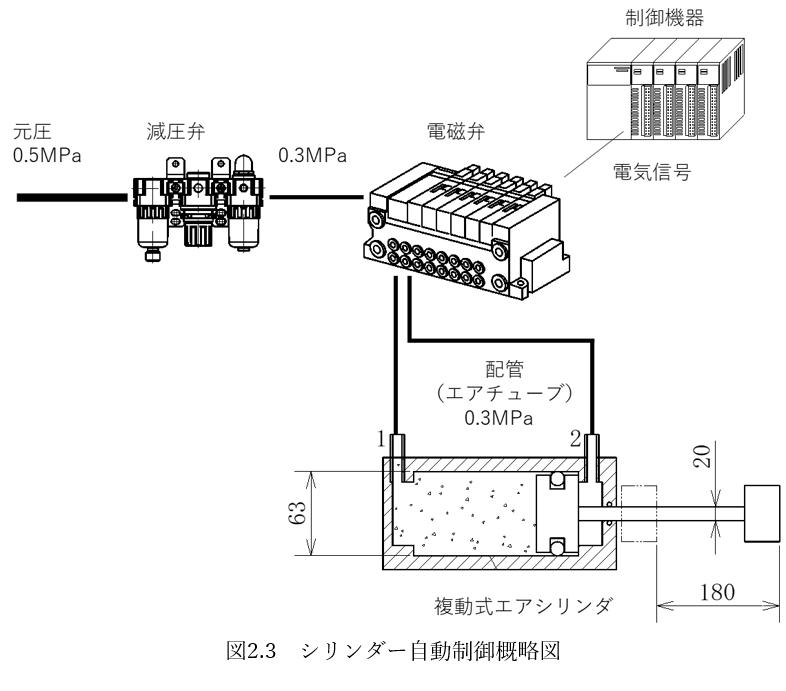
(3)チャレンジ問題(実際の設計)
複動式のエアシリンダーの動作を自動で制御するために、圧縮空気の給排気を電磁弁を使って切り替えます。電磁弁からエアシリンダーまでの配管は外径φ6、内径φ4のエアチューブで長さが約2,000です。
シリンダーは内径φ63、ロッド外形φ20、ストローク180の複動式エアシリンダーを使います。
この複動式エアシリンダーが12秒に1回のサイクルタイムで往復動作します。圧縮空気は元圧0.5MPaで供給されるものをレギュレーターで0.3MPaに絞って供給します。このとき、1分間当たりでエアシリンダーが消費する空気の体積を求めてください。
*解答はウェビナーをご確認ください。
*電磁弁についてはコラムで補足します。
コラム 電磁弁とエアシリンダー
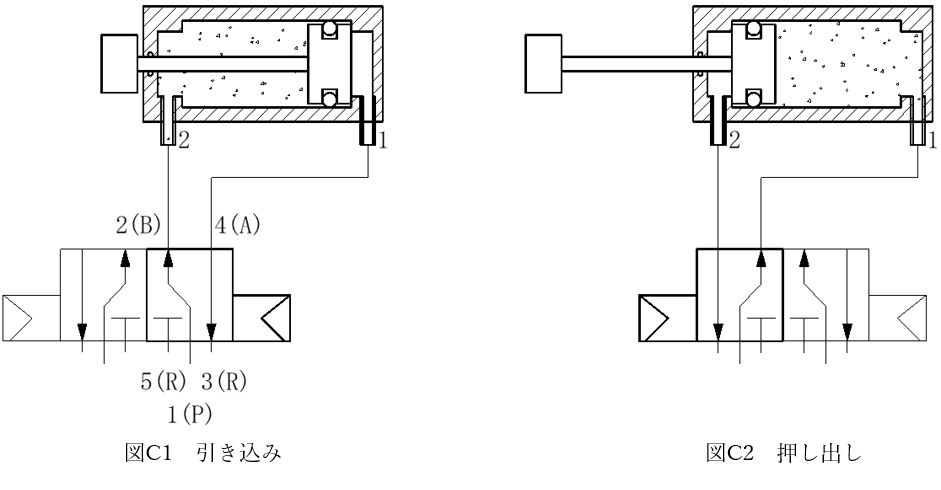
電磁弁は電気の力(電磁力)で開閉する弁です。複動式エアシリンダーの場合、基本的に5ポート(あるいは4ポート)が使用されます。
5ポート電磁弁のと複動式エアシリンダーのつなぎ方と動きのイメージを図C1および図C2に示します。各ポートの接続は次の通りです。
*つなぎ方は必ずこの通りにしなければならないというものではありません。
1番ポート : 圧縮空気
2番ポート : シリンダー2番ポート
3番ポート : 排気(大気開放)
4番ポート : シリンダー1番ポート
5番ポート : 排気(大気開放)
図C1は電磁弁右側のソレノイドをオン、左側のソレノイドをオフにした状態です。このとき圧縮空気はエアシリンダーの2番に給気され、エアシリンダーの1番は排気されます。よってロッドは引き込まれます。
電気信号を入れ替えて図C2のように右側のソレノイドをオフ、左側のソレノイドをオンにすると給気排気が入れ替わりロッドが押し出されます。
それぞれの動作における排気は配管を通って電磁弁から排気されます。