プラスチック製品の強度設計基礎講座 第2回 基本的な強度計算の方法
本連載では、技術士の田口先生による「プラスチック製品の強度設計基礎講座」を行います。入社5~6年までのプラスチック製品設計者の方や、プラスチック製品の設計方法を学びたい材料メーカー、
今回は第2回 基本的な強度計算の方法について解説いたします。
目次
1.はじめに
今回は材料力学の中でも基本的な、引張、圧縮、曲げ荷重の強度計算方法について解説します。材料がプラスチックでも金属でも計算方法は基本的に同じです。
2.引張荷重/圧縮荷重の強度計算
引張、圧縮荷重の応力や変形量は、図1の垂直応力の定義、垂直ひずみの定義、フックの法則の3つを使用することにより、簡単に計算することができます。
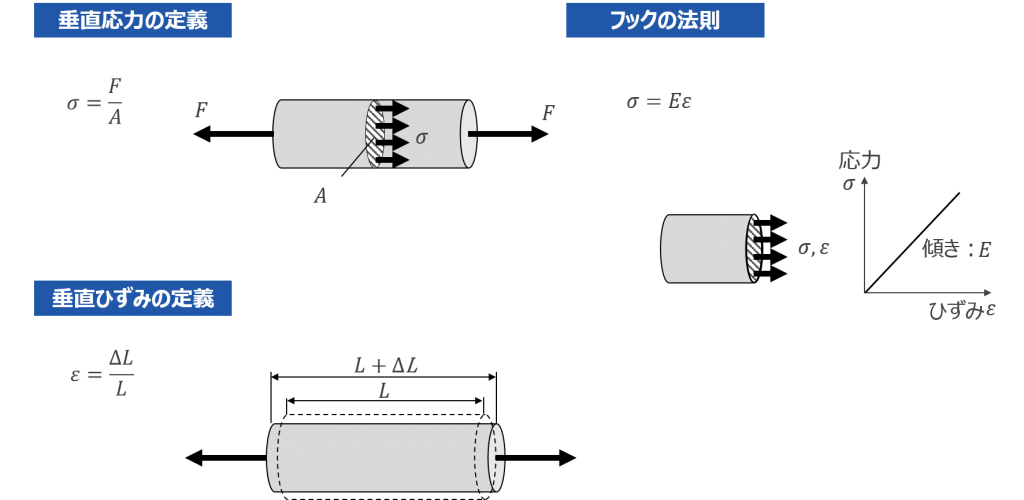
図 1 垂直応力/垂直ひずみ/フックの法則
図2のような丸棒に引張荷重が与えられた場合について、実際に計算してみましょう。
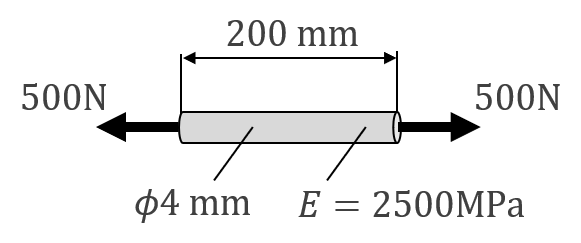 |
| 図 2 引張荷重を受ける丸棒 |
垂直応力の定義より
\[
\sigma = \frac{F}{A}
\]
\[
\sigma = \frac{F}{A} = \frac{500}{3.14×2^2} ≒ 39.8 MPa
\]
フックの法則より
\[
\sigma = E\varepsilon
\]
\[
\varepsilon = \frac{\sigma}{E} ・・・①
\]
垂直ひずみの定義より
\[
\varepsilon = \frac{\Delta L}{L}
\]
\[
\Delta L = \varepsilon L ・・・②
\]
①、②より
\[
\Delta L = \varepsilon L = \frac{\sigma L}{E} ・・・③
\]
\[
\Delta L = \frac{\sigma L}{E} = \frac{39.8×200}{2500} ≒ 3.18mm
\]
このように簡単に応力と変形量を求めることができます。
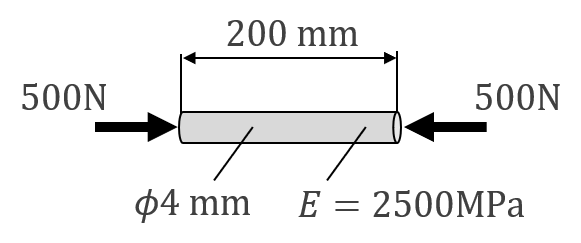 |
| 図 3 圧縮荷重を受ける丸棒 |
次に圧縮荷重の強度計算をしてみましょう。引張荷重と同様に丸棒に圧縮荷重が与えられた場合で考えます(図3)。
垂直応力は圧縮荷重の場合、符号が負になるため
\[
\sigma = -\frac{F}{A}
\]
\[
\sigma = -\frac{F}{A} = -\frac{500}{3.14×2^2} ≒ -39.8MPa
\]
引張荷重と同様に計算できるので、式③より
\[
\Delta L = \frac{\sigma L}{E} = \frac{-39.8×200}{2500} ≒ -3.18mm
\]
引張荷重と圧縮荷重の計算方法は全く同じですが、符号が変わることに注意しましょう。圧縮荷重を計算する際に、もうひとつ注意しなければならないことがあります。それは座屈です(図4)。プラスチック製の定規を引っ張っても、人の力で破断させることはできませんが、圧縮方向に力を加えると、大きく湾曲し、人の力でも壊すことができます。このように、細長い物体に圧縮荷重を加えたとき、大きく変形する現象を座屈といいます。座屈は細長い物体に圧縮荷重を加えたときに生じる現象で、太くて短い物体や引張荷重では起きません。また、座屈は縦弾性係数が小さいほど発生しやすい現象です。したがって、プラスチックは、金属に比べて座屈が起きやすい材料だといえます。

図 4 座屈
3.曲げ荷重の強度計算(はりの強度計算)
主に曲げ荷重を受ける長い部材をはりといいます。曲げ荷重は同じ大きさの引張荷重やせん断荷重などに比べると、物体への影響が大きいため、強度設計においては非常に重要な荷重です。また、強度計算の方法は引張荷重のように簡単ではなく、学校などで習っていても苦手だという方が多いかもしれません。
3-1 はりの強度計算の3ステップ
図5のように、3つのステップに分けて考えることによって、はりの強度計算ができるようになります。
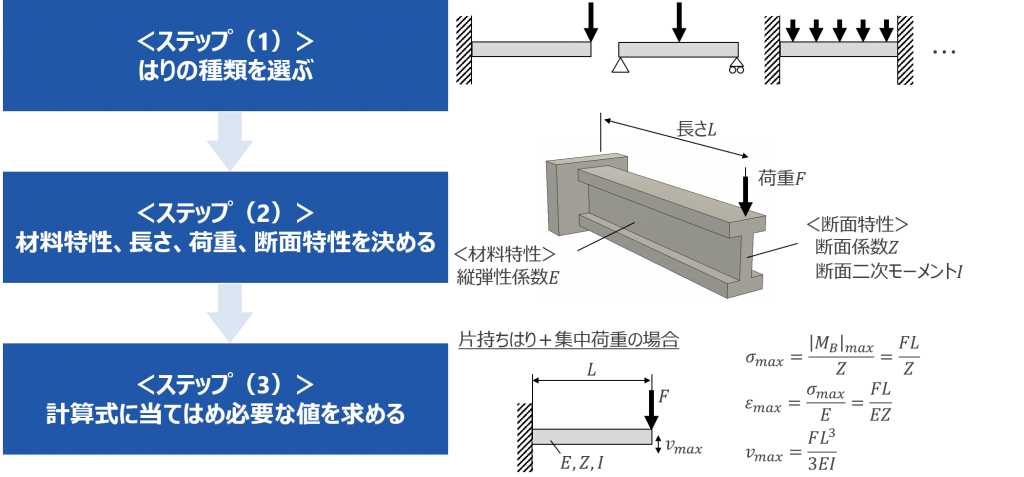
図 5 はりの強度計算の3ステップ
<ステップ(1) はりの種類を選ぶ>
強度計算を実施する製品の条件をモデル化できそうなはりの種類を選びます。同じ大きさの荷重でも、はりの種類ごとに強度計算式が異なるため、慎重にはりの種類を選ぶ必要があります。計算式自体は教科書などに公式として掲載されていますので、覚える必要はありません。
<ステップ(2) 材料特性、長さ、荷重、断面特性を決める>
次に、はりの材料特性、長さ、荷重(またはモーメント)、断面特性を決めます。断面特性で必要になるのは断面係数 \( Z \)と断面二次モーメント \( I \)です。\(Z、 I \) の決め方によって、生じる応力、たわみが大きく変わってきます。\(Z、 I \)も教科書などに一覧で掲載されていますので、覚える必要はありません。
<ステップ(3) 計算式に当てはめ必要な値を求める>
ステップ(1)で決めたはりの種類について、公式に値を当てはめ応力やたわみを計算します。使用する値はステップ(2)で決めたものだけです。図5ステップ(3)の計算式を見ると分かるように、非常に簡単な計算式ではりに発生する応力、ひずみ、たわみを計算することが可能です。ただし、はりのどの部分に、どのような応力が生じているかなど、いくつか理解しなければならないことがあります。次項からそれらについて解説していきます。はりの計算の進め方が分かったら、例題を解いて理解を深めてください。
3-2 はりの種類
はりの種類は支持条件と荷重条件によって決まります。支持条件は固定支持、単純支持(回転支持、移動支持)、自由端があります。モーメント(回転)と水平・垂直方向の力を支持部でどう伝えるかがポイントです。荷重条件には集中荷重、分布荷重、モーメント荷重がそれぞれ、はりのどの位置にいくつ作用するかについて考えます。これらの支持条件と荷重条件の組合せにより、はりの種類が決定します。はりの種類は無限に作り出すことができますが、片持ち、両端単純支持、両端固定支持が代表的なはりとして教科書などでよく紹介されています。
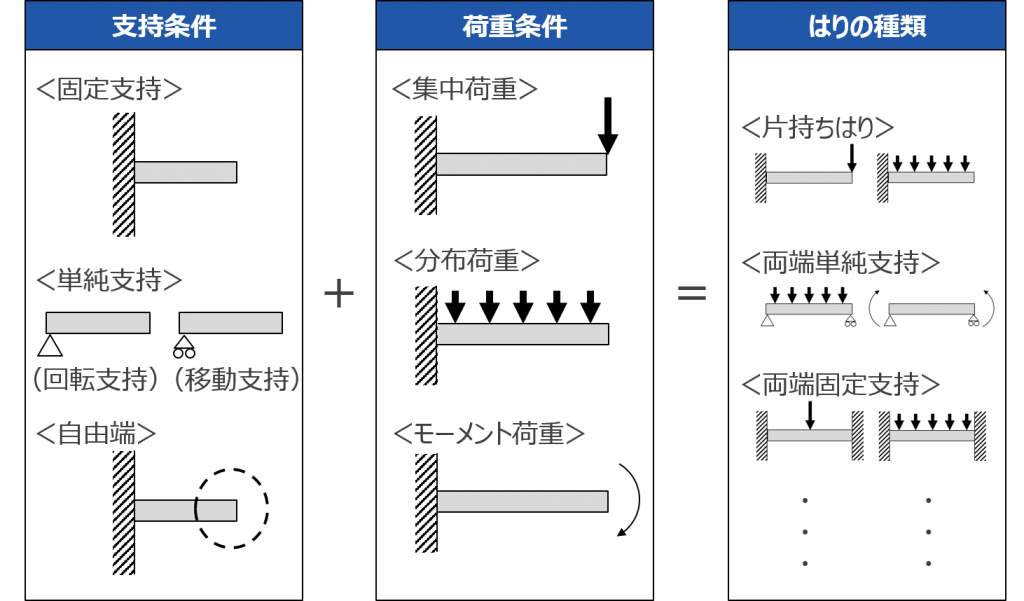
図 6 はりの種類
3-3 曲げモーメント
図7のようにはりの一部を取り出して考えたとき、その部分には曲げモーメントとせん断力が生じています。はりの強度計算を行う場合、せん断力の影響は非常に小さいため、厳密な計算を行う場合や、はりが極端に短い場合を除き無視しても構いません。したがって、はりの強度計算では曲げモーメントに着目し、曲げモーメントによって応力やたわみが発生すると考えます。
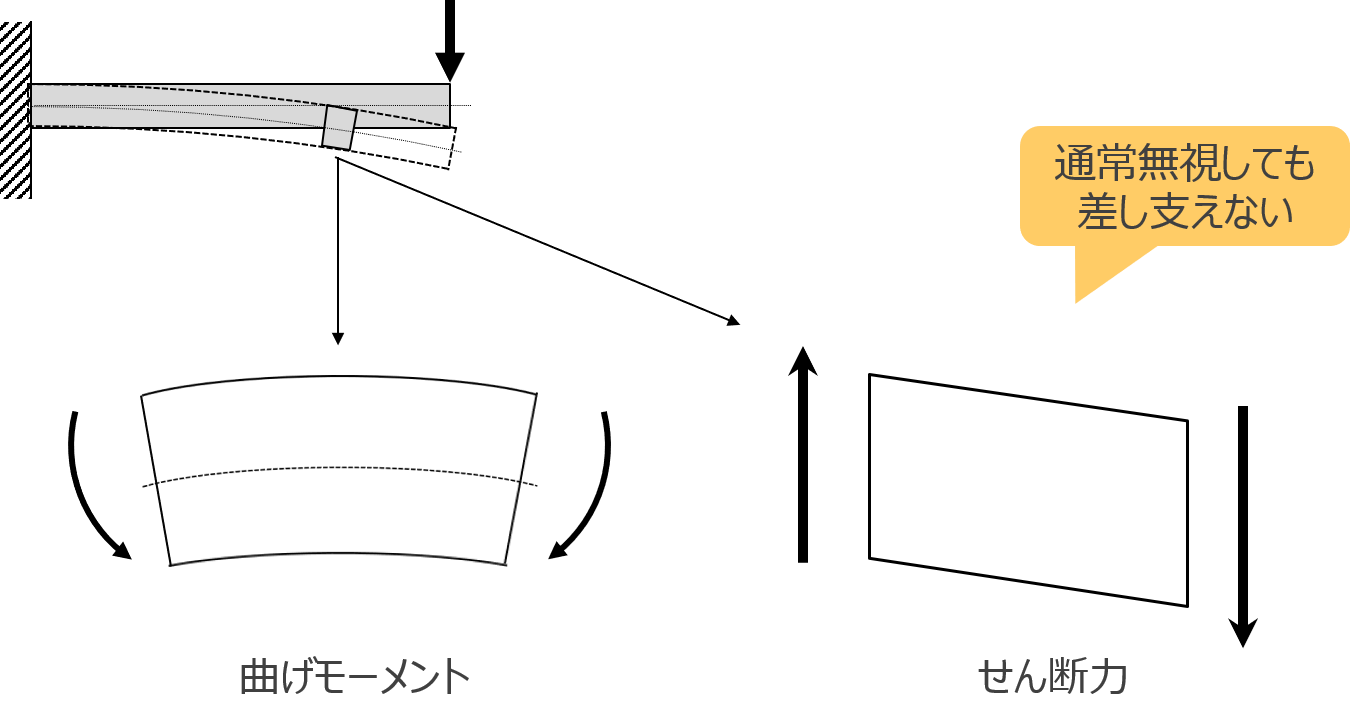
図 7 曲げモーメントとせん断力
図8の向きに曲げモーメント\(M_B \) が作用すると、はりの上面は引っ張られて伸び、下面は圧縮されて縮みます。はりの中央付近には伸びも縮みもせず、応力も生じない面が存在します。この面のことを中立面といいます。また、はりの任意の断面と中立面の交線を中立軸といいます。中立軸は断面の図心(重心)を通ります。中立面から外側に行くほど応力は大きくなり、上面の一番外側で引張応力の最大値、下面の一番外側で圧縮応力の最大値となります。このように曲げモーメントが作用することによって生じる引張応力と圧縮応力のことを曲げ応力といいます。曲げ応力という全く別の応力があるわけではありません。

図 8 曲げ応力
曲げモーメントは下側が引張応力になる方向と、上側が引張応力になる方向の2つが存在します。引張応力と圧縮応力はいずれも垂直応力ですが、多くの材料が引張と圧縮では特性が異なるため、どちらの応力が生じているかを把握しておく必要があります。そこで、下側が引張応力になる方向を正、上側が引張応力になる方向を負と約束することにします(本稿における約束)。

図 9 曲げモーメントの正負の約束
この約束にしたがって、実際のはりにどのような曲げモーメントが生じているのかを見てみましょう。図10の①のように片持ちはりの先端に集中荷重が加えられた場合、全体に渡って上側に引張応力が生じることは容易にイメージできると思います。したがって、曲げモーメントは全体に渡って負となります。②の両端単純支持の場合は、片持ちはりの反対で下側全体が引張応力になります。つまり、曲げモーメントは全体に渡って正です。③の両端固定支持の場合は少し複雑です。中央部分は下側に引張応力が生じ、両端部分では上側に引張応力が生じます。したがって、曲げモーメントは中央部分で正、両端部分で負となります。

図 10 曲げモーメントの向きの様子
シンプルなはりであれば、曲げモーメントの向きはすぐに分かります。しかし、荷重が複数あるなど、複雑になってくると少し難しくなります。また、曲げモーメントの向きだけではなく、はりのどの部分で大きな曲げモーメントが生じているかも把握する必要があります。そこで、はりに生じる曲げモーメントの様子を分かりやすく示した曲げモーメント図を利用します(図11)。片持ちはりの場合、全体に渡って曲げモーメントが負であることは前述した通りですが、曲げモーメント図を見ると、固定端(壁部分)で負の最大値、先端でゼロになることが分かります。両端単純支持のはりの場合は、両端がゼロで、中央部分で最大です。両端固定支持のはりの場合は、中央部分が正の最大値、両端が負の最大値となります。正の最大値と負の最大値の間には曲げモーメントがゼロになる部分があることが曲げモーメント図から見て取れます。
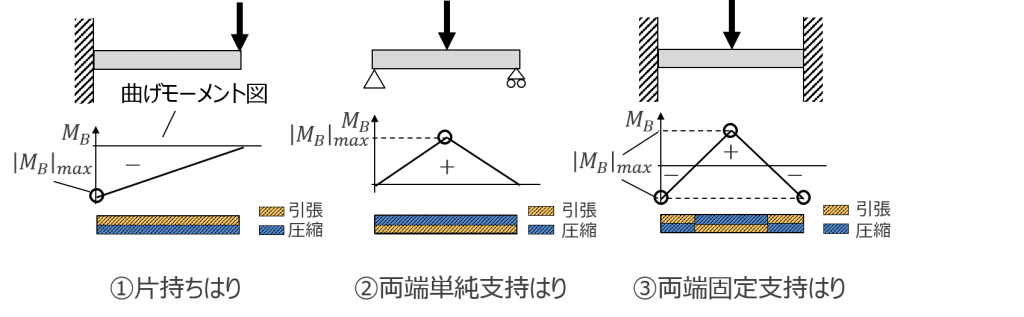
図 11 曲げモーメント図
曲げモーメント図を読み取る際のポイントを図12にまとめています。はりの強度計算をするときに最も重要な値である最大応力は、最大曲げモーメント\(|M_B|_{max} \) の位置で生じます。\(|M_B|_{max} \) は教科書などに載っている公式を利用します。曲げ応力は曲げモーメントによって生じますので、曲げモーメントがゼロの部分は曲げ応力もゼロとなります。曲げモーメントが正の部分では下側に引張応力が、負の部分では上側に引張応力が生じています。

図 12 曲げモーメント図を読み取るポイント
3-4 断面係数とはりに発生する応力
最大曲げモーメント\(|M_B|_{max} \) に加えてはりの断面特性が分かれば、はりに生じる応力を計算できるようになります。応力計算に必要な断面特性が断面係数\(Z \) です。断面係数は曲げ応力の生じにくさを表し、他の条件が同じであれば、断面係数が大きいほど曲げ応力は小さくなります。ここでは例として長方形断面と三角形断面の断面係数の特徴について見てみましょう(図13)。長方形断面も三角形断面も、幅方向\(b \) を大きくするよりも、高さ方向 を大きくした方が、効果的に断面係数を大きくすることができます。長方形や円のように、中立軸に関して対称な形状の場合は、断面係数は1つだけしかありません。一方、三角形のように中立軸に関して非対称な形状の場合は、断面係数が2つ存在します。三角形断面は、上側の断面係数\(Z_2 \) が下側の断面係数 \(Z_1 \) の半分の大きさしかありません。したがって、上側でより大きな応力が生じます。
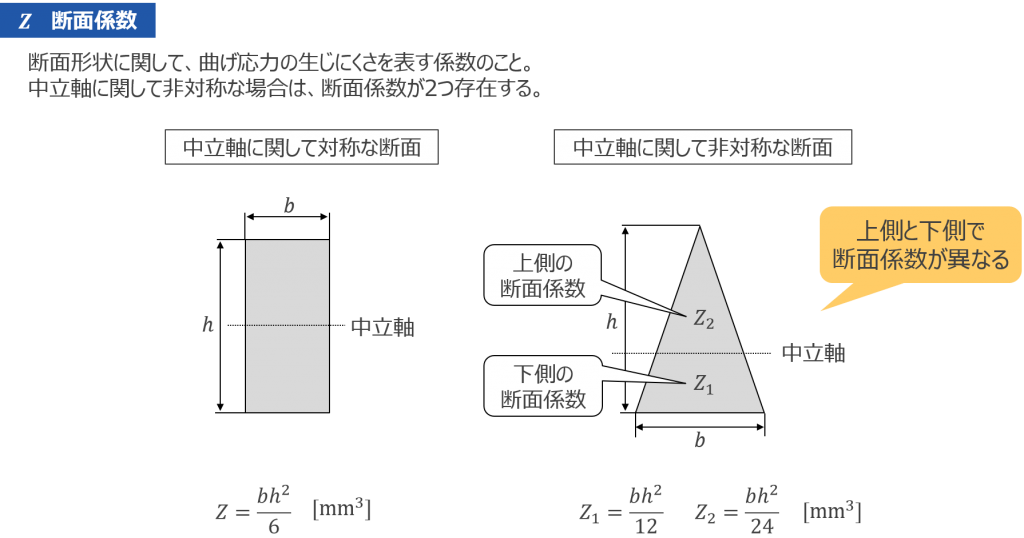
図 13 断面係数
はりに発生する応力を求めていきます。まず中立軸に関して対称な長方形断面について、 \(M_B > 0 \) すなわち下側に引張応力が生じる向きに曲げモーメントが作用する場合を考えてみます。任意の断面においてはりに発生する最大応力は、曲げモーメントを断面係数で割るだけで求めることができます。したがって、曲げモーメントの大きさが同じであれば、断面係数を2倍にすれば、発生応力を半分にすることができます。設計段階で断面を適切に選ぶことが非常に重要であることが分かります。また、この場合、断面の上側では圧縮応力が生じますので、符号は負になります。
次に中立軸に関して非対称な三角形断面について見てみましょう。中立軸に対して非対称な断面では、断面係数は上側と下側で異なります。上側の応力を計算する際には上側の断面係数、下側の応力は下側の断面係数を使用しなければなりません。三角形断面の場合、断面係数は\(Z_1 = 2Z_2 \) ですので、発生応力は上側が下側の2倍の大きさになることを示しています。
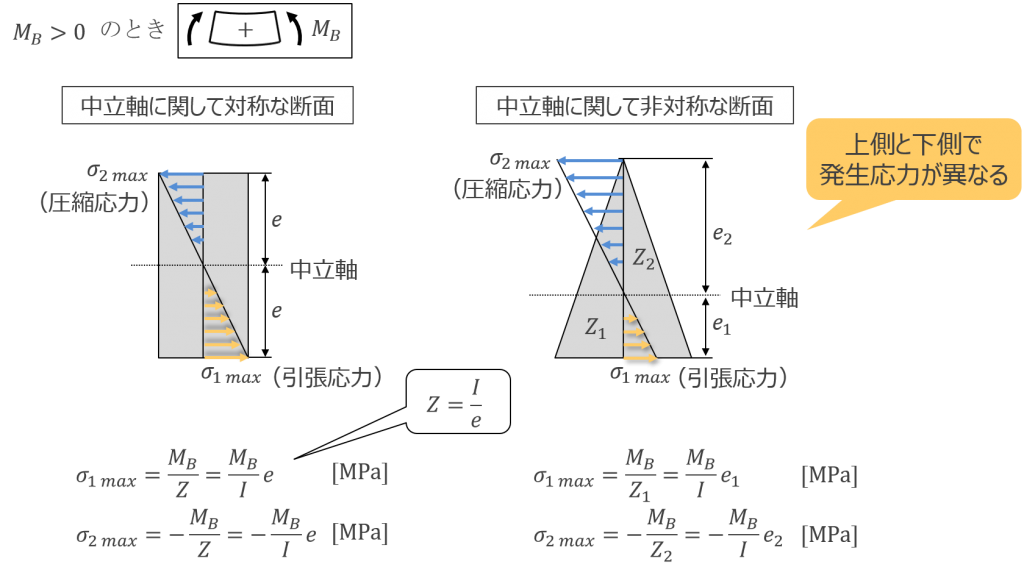
図 14 はりに発生する応力
3-5 断面二次モーメントとはりのたわみ
はりに生じる応力と同様に、たわみも断面形状に大きな影響を受けます。はりのたわみにくさを表す断面特性が断面二次モーメントIです。他の条件が同じであれば、断面二次モーメントが大きいほど、はりはたわみにくくなります。ここでも長方形断面と三角形断面について見ていきましょう。断面係数と異なり、断面二次モーメントは中立軸に関して対称でも非対称でも1つしか存在しません。断面係数と同様に幅方向\(b \) を大きくするよりも、高さ方向\(h \) を大きくした方が、効果が大きいことが分かります。断面係数の場合は、高さの2乗で効いていましたが、断面二次モーメントの場合は高さの3乗で効いてきますので、非常に大きな影響を受けます。プラスチック製の定規を曲げるとき、曲げる方向によって曲がりにくさが全く異なるのはこのためです。
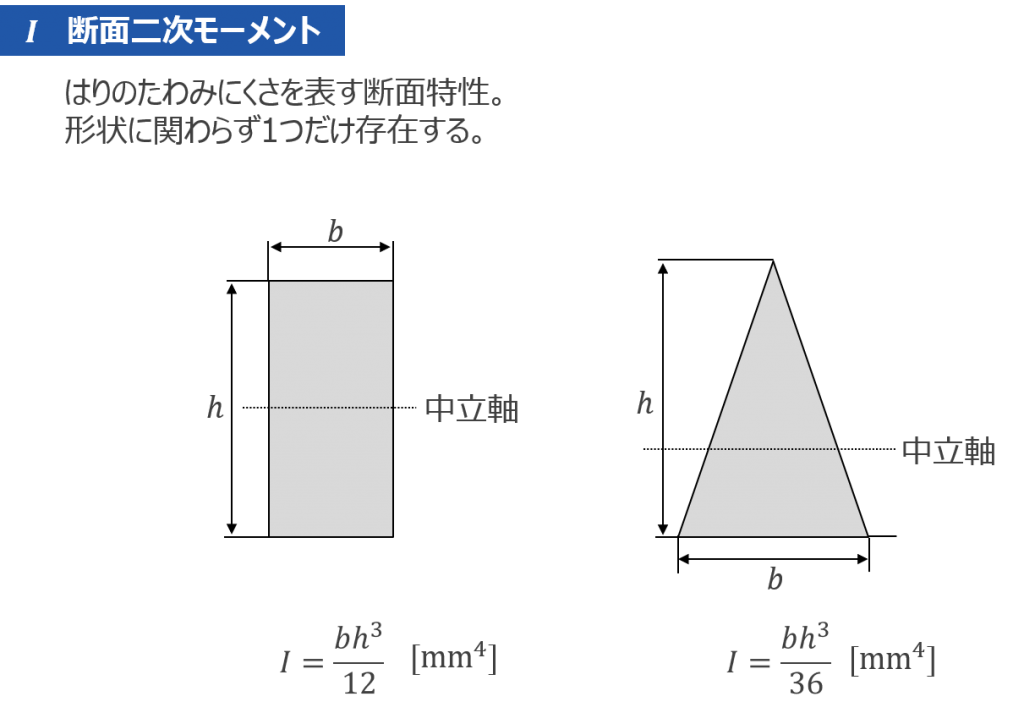
図 15 断面二次モーメント
はりは曲げ荷重を受けると曲線を描いて変形します。中立面が描く曲線の曲率半径を とすると、図16の式④のように表すことができます。 \(\rho\) が大きくなるということはたわみが小さくなることを意味しますので、曲げモーメント\(M_B\) が同じであれば、 \(EI\) が大きいほどたわみにくいはりだといえます。このときの \(EI\) をはりの曲げ剛性といいます。たわみにくいはりにするためには、縦弾性係数 \(E\) の大きな材料を使用する、断面二次モーメント \(I\) の大きな形状にする、あるいはその両方を組合せて対応します。式の導出は省きますが、式④の関係式から、はりの種類に応じたたわみ量の式を導くことができます。図16の片持ちはりの場合は式⑤のようになり、やはり式の中に曲げ剛性を示す \(EI\) が含まれています。
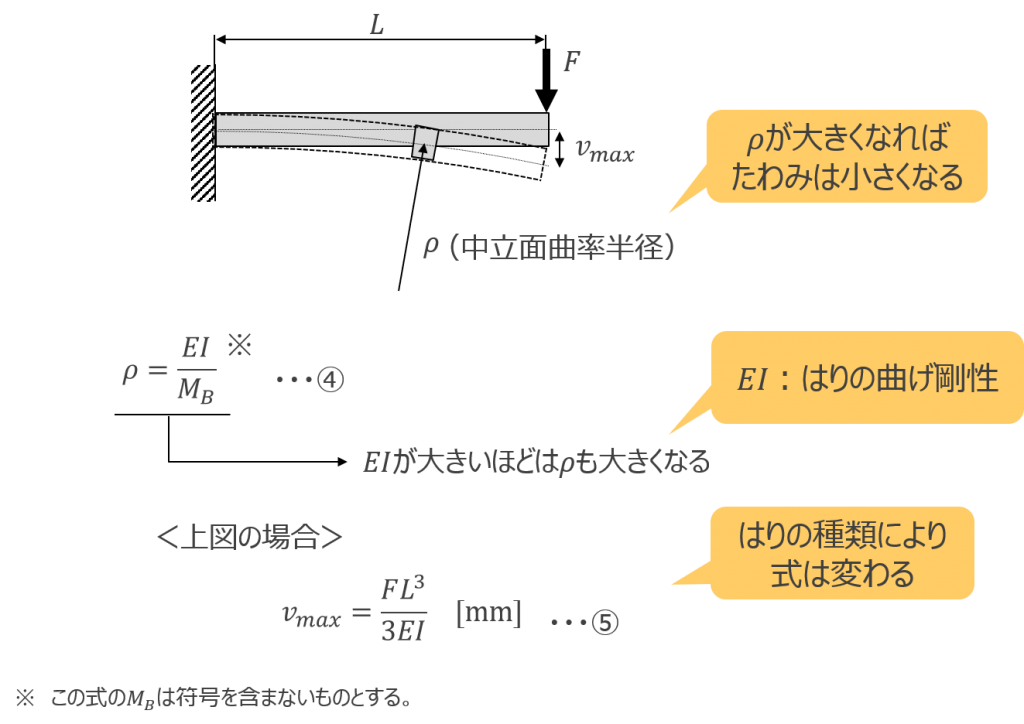
図 16 はりのたわみ
代表的なはりの強度計算式を図17に示します。
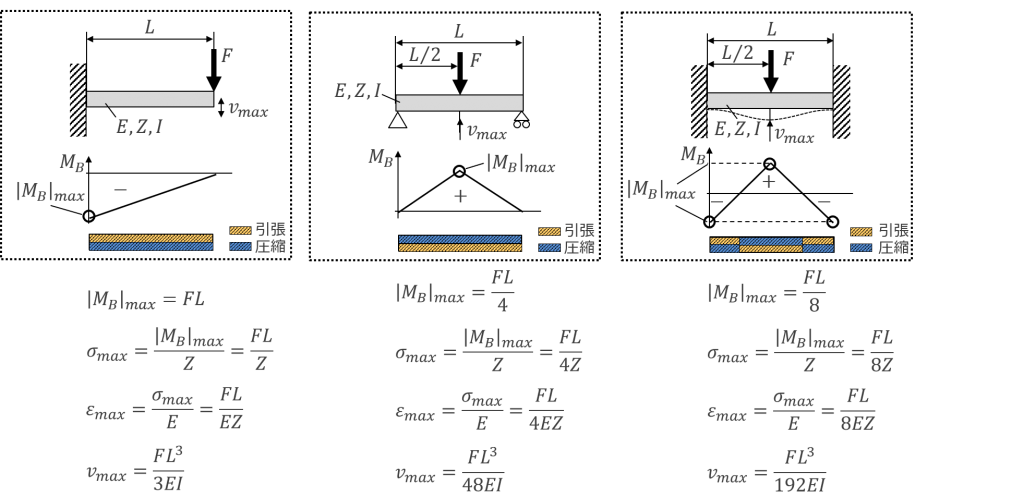
図 17 はりの強度計算式の例
4.例題-丸棒に生じる応力と伸びを求めよう
それでは片持ちはりの例題を解いてみましょう。解答はオンラインセミナーで解説します。

|
田口技術士事務所 田口 宏之 たぐち ひろゆき:大学院修士課程修了後、東陶機器㈱(現、TOTO㈱)に入社。12年間の在職中、ユニットバス、洗面化粧台、電気温水器等の水回り製品の設計・開発業務に従事。商品企画から3DCAD、CAE、製品評価、設計部門改革に至るまで、設計に関する様々な業務を経験。特にプラスチック製品の設計・開発と設計業務における未然防止・再発防止の仕組みづくりには力を注いできた。それらの経験をベースとした講演、コンサルティングには定評がある。また、設計情報サイト「製品設計知識」やオンライン講座「製品設計知識 e-learning」の運営も行っている。 |
 |


