プラスチック製品の強度設計基礎講座 第1回 材料力学の基礎とプラスチックの物性表
今回から、技術士の田口先生による新連載「プラスチック製品の強度設計基礎講座」を開始いたします。入社5~6年までのプラスチック製品設計者の方や、プラスチック製品の設計方法を学びたい材料メーカー、
今回は第1回 材料力学の基礎とプラスチックの物性表について解説いたします。
目次
1. はじめに
プラスチックは身の回りの多くの製品で利用されており、金属材料と同じぐらい身近な材料だといってよいでしょう。しかし、工業系の学校で詳しく学ぶ金属材料とは異なり、プラスチックの特性を詳しく知る機会は少ないというのが実情です。金属材料と同じような考え方で設計をしてしまうと、思わぬトラブルに見舞われることがあります。特に強度に関わるトラブルは、重大事故につながる可能性もあり、しっかりとした強度設計が不可欠です。本講座では、4回に渡ってプラスチック製品の強度設計の基礎について解説をしていきます。第1回目の今回は、プラスチックの強度設計で考慮すべきプラスチックの特性と、材料力学の基礎事項についてプラスチックの物性表を使いながら解説します。
2. プラスチック製品の強度設計
2-1 ストレス-ストレングスモデル
強度設計とは材料力学などの工学知識や、実務ノウハウを駆使しながら壊れない製品にするための設計方法です。材料力学の複雑な計算式を思い浮かべて、難しそうだなと感じる方も多いかもしれません。しかし、製品が壊れないように設計するための考え方自体は、非常にシンプルです。図1に示すように、材料強度が製品に発生する応力よりも大きくなるようにすればよいだけです。何となくできそうな気がするのではないでしょうか。製品に発生する応力を知るためには、材料力学の基礎を理解し、強度計算式を使えるようになる必要があります。材料強度を知るためには、使用する材料の強度特性を学ばなければなりません。まずは、プラスチックの強度特性についてみていきましょう。
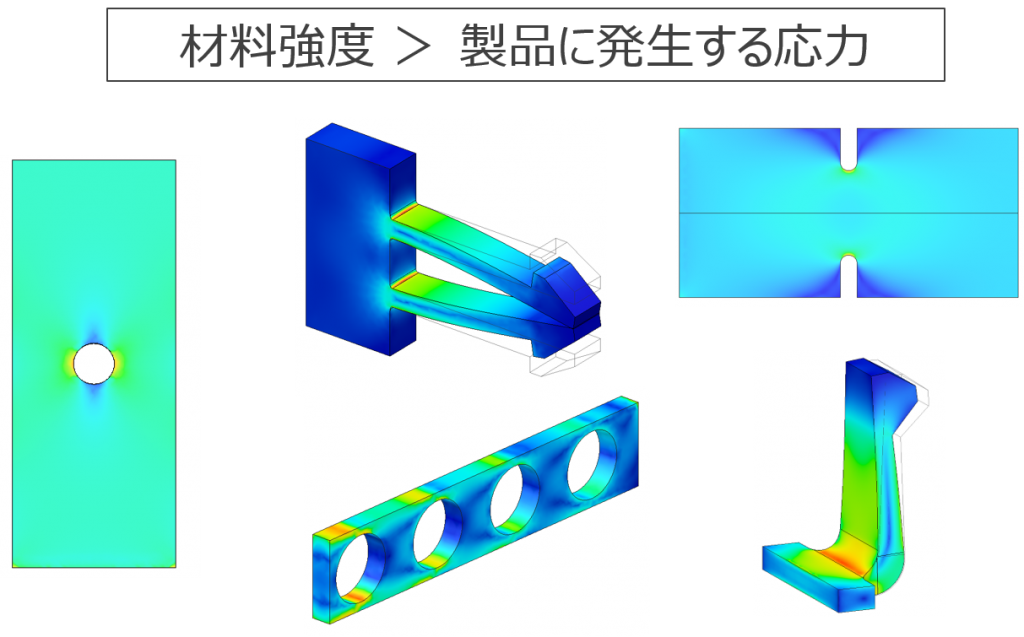
図 1 壊れない製品を設計するには
プラスチックの材料強度を考える際に重要なことの一つは、物性表に記載されている材料強度は、あくまで代表値に過ぎないことを認識しておくことです。材料メーカー各社の物性表をよく見てみてください。備考欄などに必ず「代表値であり、保証値ではありません」という主旨の但し書きが書いてあります。金属材料の多くがJIS規格などによって材料強度の最低値が保証されていることを考えると、強度設計の進め方が金属材料とは大きく異なることがわかります。プラスチックに限ったことではありませんが、プラスチックの場合は特に、図2に示すストレス-ストレングスモデルの考え方で強度設計を行うことが非常に重要です。
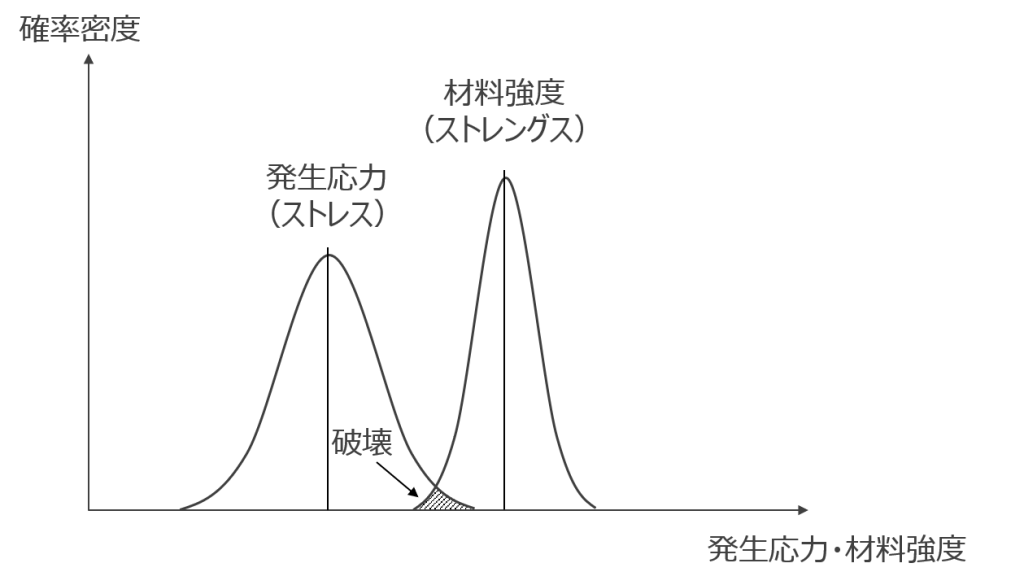
図 2 ストレスーストレングスモデル
ストレス-ストレングスモデルとは、発生応力(ストレス)と材料強度(ストレングス)の確率分布が交差する部分で破壊が生じるとする考え方のことです。金属材料の強度には当然ばらつきがありますが、材料メーカーがばらつきを踏まえた上で最低値を保証しているため、材料強度のばらつきを意識せずに強度設計を行うことが可能です。しかし、プラスチックは材料強度の最低値が保証されていないため、ばらつきを考慮した強度設計が不可欠です。
2-2 プラスチックの強度特性の特徴
金属材料はJIS規格などが整備されていることもあり、単純に静的な力(ゆっくり作用する力)によって金属製品が壊れるというようなことはほとんどありません。通常問題になるのは、腐食による材料強度の低下と、繰り返し荷重による疲労破壊です。一方、プラスチックの場合は、腐食は生じませんが、金属材料では問題になりにくい複数の欠点があります。図3の強度特性の特徴を見てみましょう。
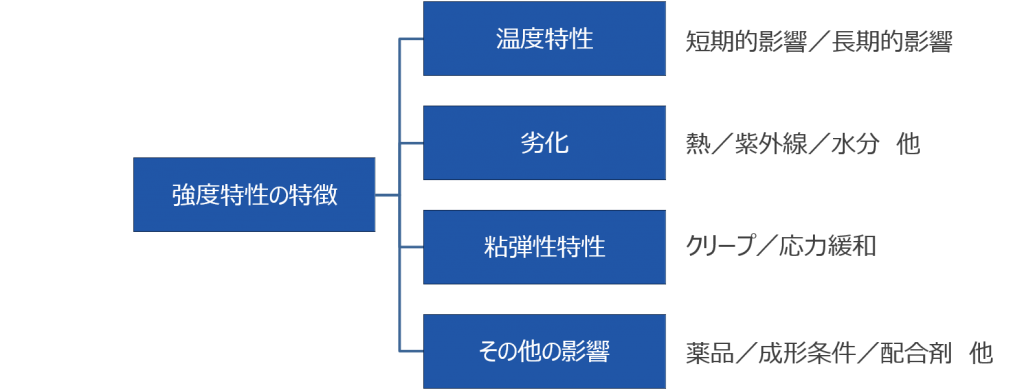
図 3 プラスチックの強度特性の特徴
まず、温度特性です。プラスチック製の容器を使って電子レンジで食品を温めると、容器の温度が上昇し柔らかくなっているという経験をしたことがあると思います。プラスチックは温度に非常に敏感で、室温からわずかに温度が上下しただけで、その強度特性が大きく変化するという特徴があります。これが温度の短期的影響です。また、次に解説する劣化や粘弾性特性といった長期的に生じる現象も温度に大きな影響を受けます。プラスチック製品では、使用する温度の上限と下限を明確に設定した上で、強度設計を行うことが求められます。
プラスチックは熱、紫外線、水分、薬品などの要因によって劣化が生じます。劣化が起きると、強度が低下します。熱、水分といった劣化要因が全くない環境はあり得ないため、すべてのプラスチック製品は劣化していく運命を持っています。したがって、例えば10年間使用する製品であれば、10年間の強度低下を加味した強度設計を行うことが必要です。
次に粘弾性特性です。粘弾性特性により生じる現象の代表例がクリープです。長期に渡って力が作用したときに、変形が徐々に大きくなり、条件によっては最終的に破断に至ることがあります。長期間に渡り力が作用し続けるような製品の場合、クリープ強度の評価をしなければなりません。温度特性、劣化、粘弾性特性については、第3回、第4回の講座で詳しく解説する予定です。他にも薬品や成形条件、配合剤など影響を受ける条件は多様です。このようにプラスチックは非常に繊細な材料であり、色々な面で配慮する必要があるのです。
3. プラスチックの物性表と一緒に学ぶ材料力学の基礎
3-1 荷重/応力/ひずみ
製品に発生する応力を把握するためには、材料力学の基礎を理解する必要があります。ここからはプラスチックの物性表と一緒に、材料力学の基礎について解説していきます。
プラスチックの物性表に掲載されている基本的な強度特性として、図4のように引張特性と曲げ特性があります。まず、これらの基本的な特性の意味が理解できるように、材料力学の基本である荷重、応力、ひずみの意味を理解しましょう。
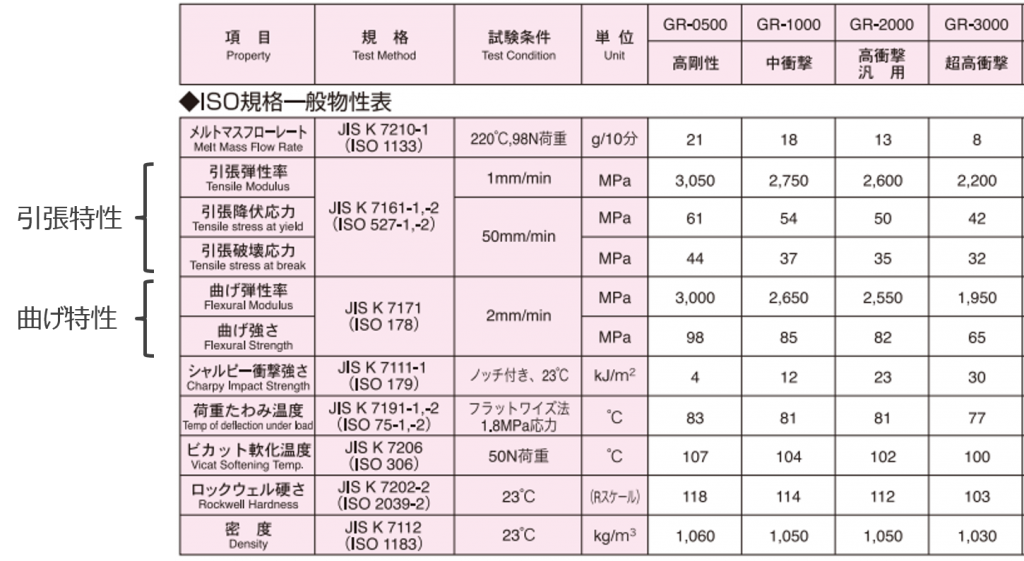
図 4 ABS物性表(出所:デンカ株式会社)
<荷重>
物体は荷重という外力を受けて変形したり、壊れたりします。同じ大きさの荷重でも、その種類や形態が異なると、物体への影響が違ってきます。例えば、割り箸を手で引きちぎろうとしても困難ですが、親指を割り箸の中央付近に当てて力を入れると、簡単に折ることができます。人の力はそれほど変わらないはずですが、荷重のかけ方で物体への影響が異なることがわかると思います。
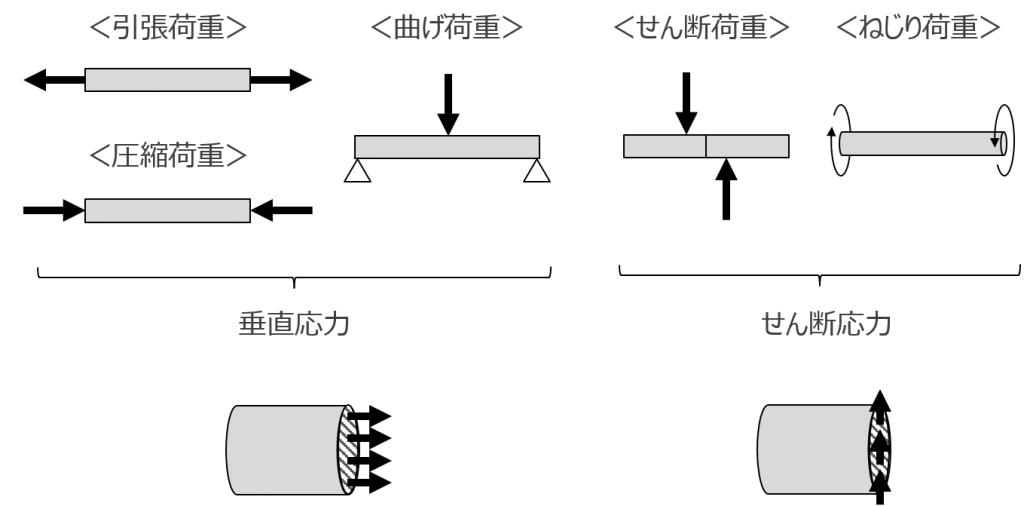
図 5 荷重の種類
荷重には様々なものがあります。分類方法の一つとして、垂直応力を生じる荷重と、せん断応力を生じる荷重に分けることができます。図5に示すように、主に垂直応力を生じる荷重に引張荷重、圧縮荷重、曲げ荷重、せん断応力を生じる荷重にせん断荷重とねじり荷重があります。同じ材料でも垂直応力とせん断応力では影響が異なるため、どのような荷重により、どのような応力が生じているかを把握しなければなりません。応力の定義については次に解説します。
<応力>
荷重が物体に与える影響や、材料強度を表すために使う指標が応力です。図6に示すように、応力は荷重が作用している物体を仮想的に切断したとき、その仮想断面における単位面積当たりの内力として定義されます。内力とは物体を仮想的に切り離したときに、荷重Fとつり合うように仮想断面に生じる力のことです。内力が大きいほど物体への影響が大きくなると考えられますが、内力が大きくても物体も大きければ、影響はさほど大きくありません。また、内力が小さくても、物体が小さければ、影響が大きくなる可能性があります。したがって、荷重が作用したときの物体への影響は内力の大きさではなく、単位面積当たりの内力である応力で評価した方が便利です。物体の大きさにかかわらず、応力が大きいほど、物体への影響が大きくなるといえます。図6に示す応力は仮想断面に対して垂直方向ですので、垂直応力を示しています。仮想断面に沿う方向の応力をせん断応力といいます。
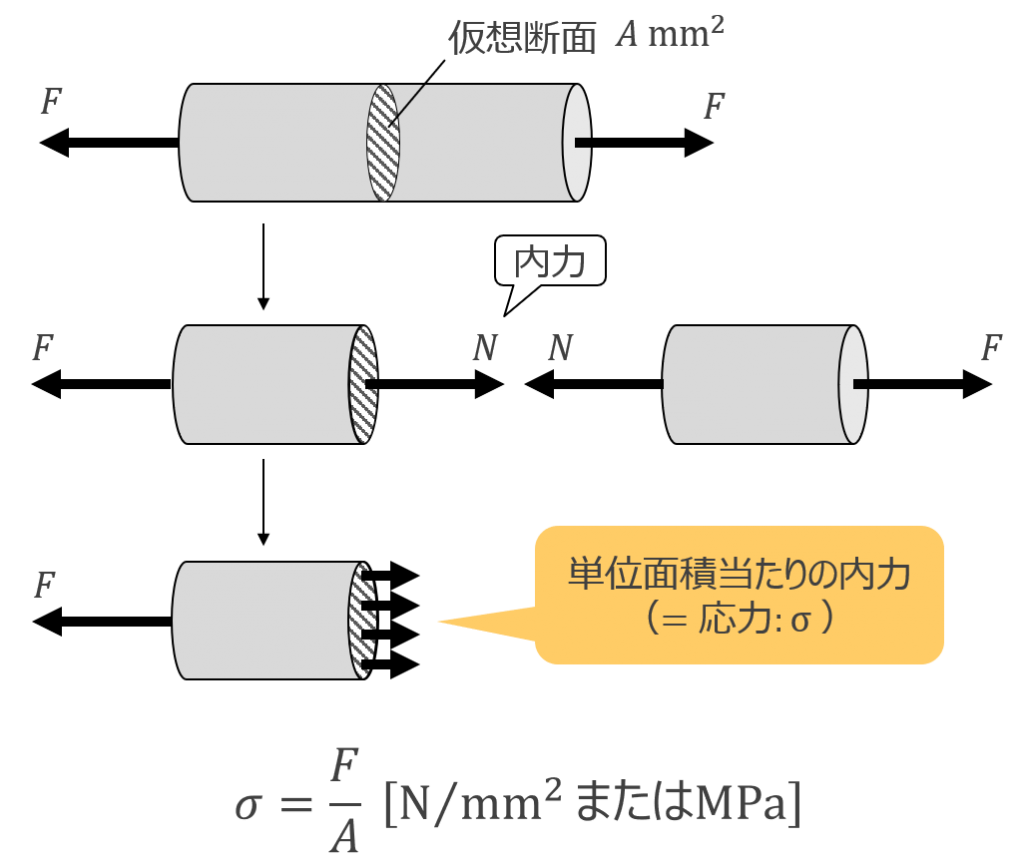
図 6 応力の定義
図4の物性表における「引張降伏応力」「引張破壊応力」「曲げ応力」は、引張荷重、曲げ荷重が作用した際の材料強度を応力という考え方を使って示した指標です。これらの意味については第3回の講座で解説予定です。ちなみに図5で示したように引張荷重、曲げ荷重で生じる応力は垂直応力ですので、「引張降伏応力」「引張破壊応力」「曲げ応力」は垂直応力のことを表しています。
図7に示すようにプラスチックは金属材料と比べると強度が大きく劣ります。ただし、プラスチックは軽いため、重さあたりの強度で比較すると、金属材料との差は小さくなります。また、ガラス繊維や炭素繊維などを配合したプラスチックでは、重さあたりでは金属材料以上の強度にすることも可能です。そのため自動車や航空機などで軽量化を目的に多く用いられるようになっています。
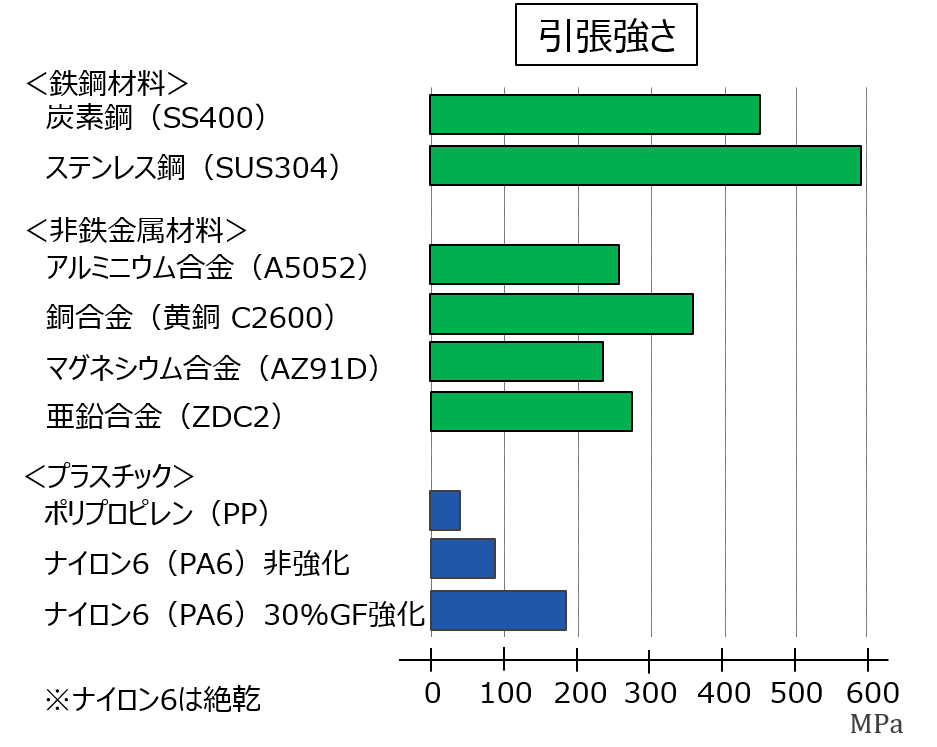
図 7 プラスチックと金属材料の強度比較
<ひずみ>
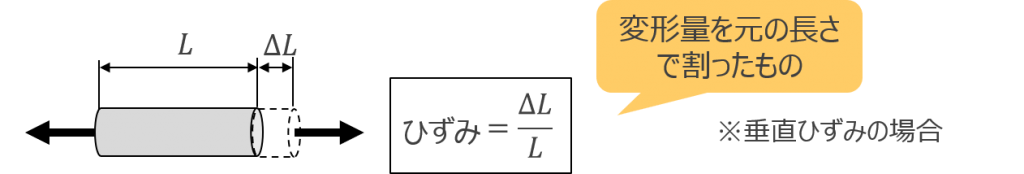
図 8 ひずみの定義
物体に荷重が加わると変形を起こします。強度設計では発生応力と合わせて、変形の大きさが重要な検証ポイントになります。変形を考える際には、変形の大きさを考えるだけでは十分ではありません。なぜなら、同じ大きさの応力が発生するような条件でも、物体の大きさによって、変形量が異なるからです。例えば、同じ断面積、材質で長さ違いの棒材を同じ荷重で引っ張ったとします。断面積と引張荷重が同じであるため、発生する応力
も同じ値になります。しかし、棒材の伸びは長い棒材の方が大きくなるのです。したがって、変形について評価するためには、変形量だけではなく、変形割合も考える必要があります。物体に荷重が作用した際の変形割合のことをひずみといいます(図8)。図8のような引張荷重の場合、変形量を元の長さで割った値がひずみです。ひずみは応力に対応して生じます。図8に示すひずみは垂直応力に対応した垂直ひずみです。せん断応力の場合には、せん断ひずみが生じます。
3-2 フックの法則
学校でばねのフックの法則を習ったことを覚えているでしょうか。荷重とばねの伸びが比例関係になるという法則です。フックの法則はばねだけではなく、プラスチックや金属材料など一般材料でも成り立つと考えることできます。ばねの場合は、荷重と伸びの関係に着目し、図9の左側のような式やグラフで考えました。このときの直線の傾きkがばねの硬さ(変形のしにくさ:ばね定数)を表しています。一般材料でも荷重と伸びに着目してもよいのですが、応力とひずみのところで解説したように、物体の大きさが変わると式も変わってしまうため、不便です。そこで荷重の代わりに応力、伸びの代わりにひずみを用いると、物体の大きさに無関係の式を導くことができます。そのようにして表したものが図9の右側の式とグラフです。このときの直線の傾きEは縦弾性係数(またはヤング率)と呼ばれ、ばね定数と同じように材料の硬さ(変形のしにくさ)を表します。材料力学のあらゆる強度計算式はフックの法則がベースですので、σ=Eεは暗記してもよいぐらい重要な式です。
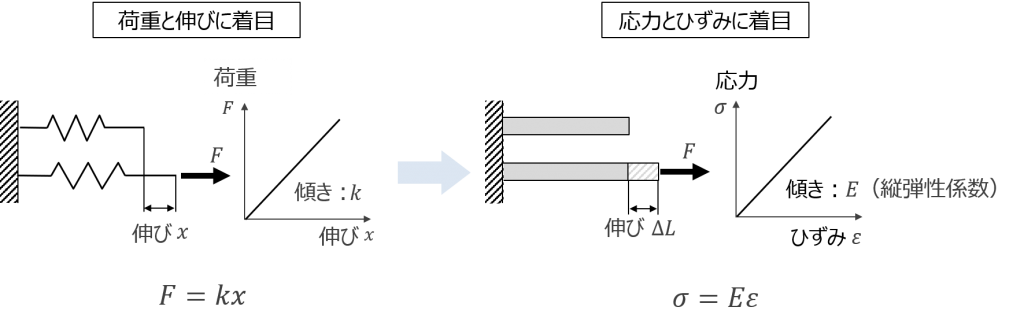
図 9 フックの法則
3-3 弾性係数
図4の物性表を見ても縦弾性係数あるいはヤング率という言葉は見当たりません。実はプラスチックでは縦弾性係数ではなく違う呼び方をします。プラスチックの場合、引張荷重試験で測定した縦弾性係数を引張弾性率、曲げ荷重試験で測定した縦弾性係数を曲げ弾性率といいます。引張弾性率も曲げ弾性率も理論的には同じ値を示すものですが、材料特性の違いなどにより微妙に異なった値となっています。ご存知の通り、プラスチックは金属材料などと比較すると柔らかい材料です。すなわち縦弾性係数が小さい材料です。図10はプラスチックとその他の材料の縦弾性係数を比較したものです。プラスチックの縦弾性係数は通常MPaという単位を使用しますが、図10では金属材料など硬い材料と比較するためGPa(MPaの1000倍)で表しています。プラスチックは材料の種類や強化繊維の配合などによって、縦弾性係数の値が大きく変わるものの、金属材料やガラスなどと比較すると、非常に小さいことがわかります。プラスチック製品では、材料の柔らかさをカバーするために、断面形状を工夫したり、リブを設けたりといった配慮が必要になります。
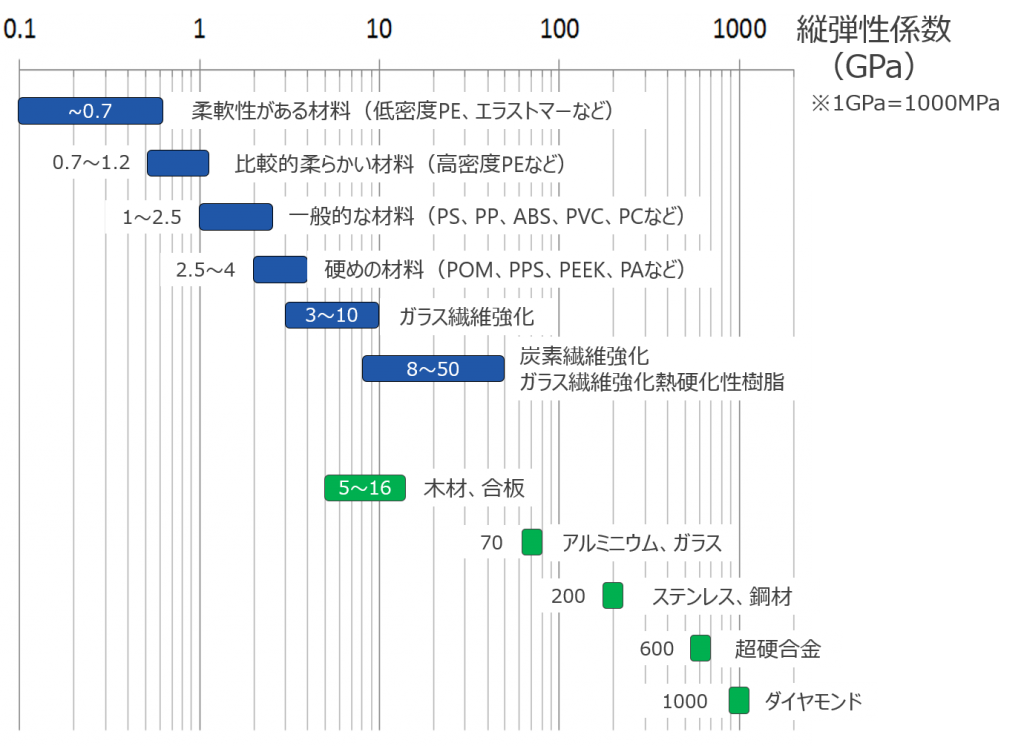
図 10 プラスチックとその他の材料の縦弾性係数
4. 例題-丸棒に生じる応力と伸びを求めよう
それでは下記例題を解いてみましょう。本稿で解説した内容だけで解くことができます(解答はオンラインセミナーで解説)。

|
田口技術士事務所 田口 宏之 たぐち ひろゆき:大学院修士課程修了後、東陶機器㈱(現、TOTO㈱)に入社。12年間の在職中、ユニットバス、洗面化粧台、電気温水器等の水回り製品の設計・開発業務に従事。商品企画から3DCAD、CAE、製品評価、設計部門改革に至るまで、設計に関する様々な業務を経験。特にプラスチック製品の設計・開発と設計業務における未然防止・再発防止の仕組みづくりには力を注いできた。それらの経験をベースとした講演、コンサルティングには定評がある。また、設計情報サイト「製品設計知識」やオンライン講座「製品設計知識 e-learning」の運営も行っている。 |
 |


