営業職が知っておきたい機械要素の基礎　第一回　歯車編

1.はじめに

皆さんが普段生活の中で使用している家電製品や自動車、電車等は多くの部品が組み合わさって出来ています。
この部品の一つ一つに目的と機能があります。そして、各部品は、国際的に標準化され、寸法や材質等は工業規格で厳密に定められています。これらの部品を総称して“機械要素”と呼びます。

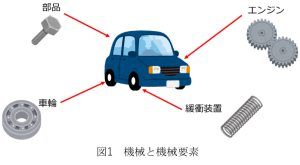
　“機械要素”にはどのようなものがあるのでしょうか。主な機械要素には、ねじ、歯車、軸受け（ベアリング）、ばね、ピン、シール部材等があります。これら機械要素はどのような役割を果たしているのでしょうか。機械要素の役割としては以下のようなものがあります。
① 締結・・・機械要素や部品同士を固定する役割を果たします。
② 回転・・・部品をスムーズに運動させる役割を果たします。
③ 伝達・・・力を伝える役割を果たします。
④ 緩衝・・・衝撃を和らげる役割を果たします。
機械要素はこれらの機能を1つまたは複数担うことで機械を機能的に動作させることができます。これから複数回に分けて商社にお勤めの方や営業職の方々にもわかりやすく機械要素について説明していきます。
第１回は“歯車”について説明していきます。

2.歯車の機能と用途

歯車には次のような機能があります。
(1)回転を伝える
　・回転を離れた場所に伝達することができる
　・回転速度を変えることができる
　・回転の方向を変えることができる
(2)動力を伝える
　・力（トルク）を伝える
　・噛み合う歯車の大きさを変えることで力（トルク）
　　の大きさを変えることができる
(3)位置を決める
　・回転量を調整することで位置決めを行うことができる

歯車の用途の一例として時計やOA機器等の駆動機構等があります。

例えば、インクジェットプリンターの内部には片面印刷や両面印刷、はがき印刷等複雑な印刷モードに対応すべく複数の歯車から構成される駆動機構を備え、用紙の供給経路を印刷モードに合わせて適宜切り替えています。

3.歯車の基礎知識

（1）歯車の種類

図4に歯車の種類を示します。歯車は大まかに“円筒歯車”、“かさ歯車”、“食い違い歯車”の３種類に分類されます。

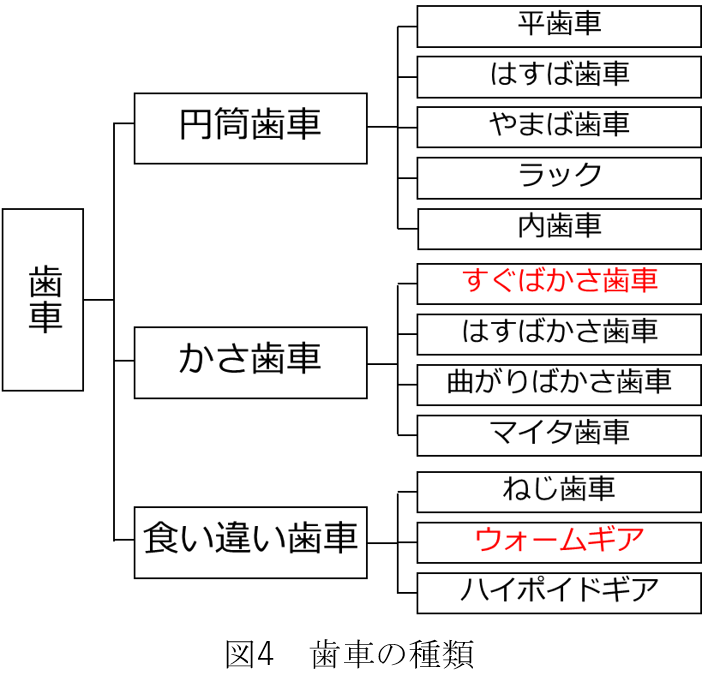
① 円筒歯車
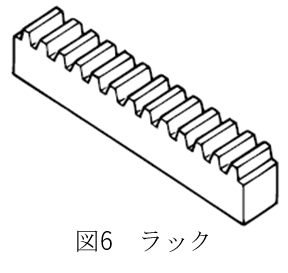
円筒歯車は、互いに噛み合う歯車の回転軸（図5一点鎖線参照）が平行な関係にあるものをいいます。円筒歯車には、歯車の中で最も一般的で歯が軸線方向に沿って真っすぐ延びている平歯車や、歯がツルマキ線上に螺旋状に形成されているはすば歯車、平らな板の上に等間隔で同じ大きさの歯が並ぶラック、円筒または円錐の内側に歯が作られている内歯車があります。

この中でも、図6に示すラックは重要で、ラックと平歯車（ピニオン）を組み合わせることでラックアンドピニオン機構というものを構成します。例えば、駆動源がモーターの場合、得られる動作は回転運動です。しかし欲しい動作が直線運動だった場合、回転運動を直線運動に変換する必要があります。ラックアンドピニオン機構は、回転運動を直線運動へ、あるいは直線運動を回転運動へと変換することができます。つまり、駆動源から得られた駆動力を適切な運動形式へと変換することができます。また、構成もラックと平歯車だけで構成されるため構成がシンプルかつコストも抑えられるので、ポピュラーな運動変換機構として広く使用されています。

② かさ歯車
かさ歯車は、互いに噛み合う歯車の回転軸（図7一点鎖線参照）が交差する関係にあるものをいいます。別名ベベルギヤとも呼ばれ、交わる２軸の角度は自由に設定できますが、直角に交わるものが多いです。これは、機械の構成上および製作上から一番精度を出しやすいのが直角だからです。

かさ歯車には、図7のように歯がまっすぐに延びているすぐばかさ歯車や、歯が曲線状に延びている曲がりばかさ歯車、２軸が直交する２個１組の歯車であるマイタ歯車があります。
マイタ歯車は、噛み合う歯車が同じ形状かつ同じ歯数のかさ歯車の組み合わせです。同じ歯数なので歯数比が1：1となり、2つの歯車が同じ回転速度で回転します。つまり、歯車間で回転速度を変えずに単に軸の回転の方向を変えて伝えるだけの時によく使われます。

③ 食い違い歯車
歯車の回転軸が互いに交わらず、かつ平行でもない歯車の総称を食い違い歯車といいます。この食い違い歯車には、ネジ歯車、ウォームギア、ハイポイドギヤがあります。
食い違い歯車の中でも図9に示すウォームギアは、円筒状の外周面にらせん状の歯を形成したウォームと、これに噛み合うウォームホイールからなる歯車を指しています。ウォームギアは、ほかの歯車が転がり接触しているのに対し、滑り接触をしています。このため、熱が発生し機械効率が悪くなる一方で、動作時の音が静かであるという特徴を有しています。さらに、非可逆性の特徴を有しています。これは通常１対の歯車のどちらを駆動させても対となる歯車に回転が伝達されますが、ウォームギアの場合、ウォーム側からしか回転が伝達されないという特徴です。つまり、動力を一方向のみに伝えたい場合に使用されます。

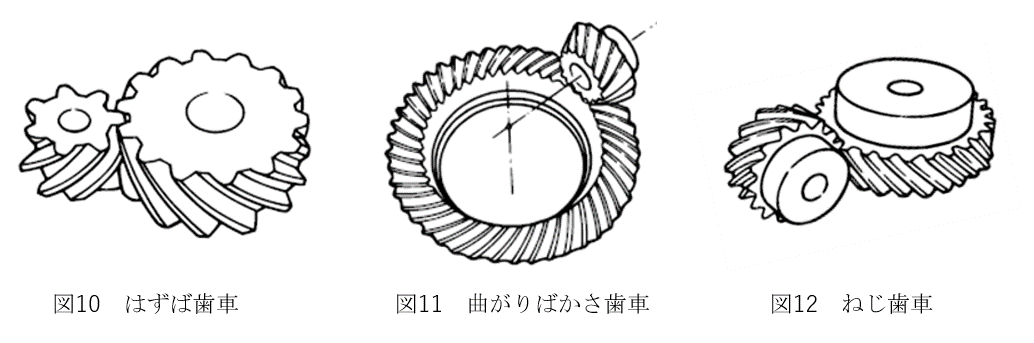
また、円筒歯車、かさ歯車、食い違い歯車において歯が延びる方向が真っすぐでなく、らせん状に湾曲しているものがあります。例えば、円筒歯車のはすば歯車（図10）、かさ歯車の曲がりばかさ歯車（図11）、食い違い歯車のねじ歯車（図12）等があります。歯をらせん状に湾曲させることで、歯が真っすぐな平歯車に比べて歯車同士の噛み合い率が向上し、強度が向上するとともに騒音を抑制することができるという特徴があります。一方で、平歯車に比べて歯を作るのに手間がかかるので平歯車に比べて価格が高くなるというデメリットがあります。

（2）歯車で覚えるべきポイント

歯車で覚えておかなければならないポイントは以下の3つです。

① ピッチ円直径
② モジュール
③ バックラッシ

① ピッチ円直径とは
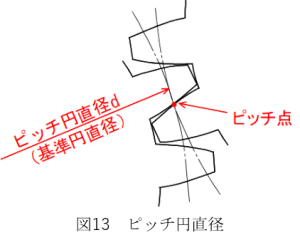
ピッチ円直径は、歯車と歯車とが噛み合う点（ピッチ点）を結んだ円のことです。基準円直径とも言います。ピッチ円直径は、歯車と歯車とが噛み合う点（ピッチ点）を結んだ円のことです。基準円直径とも言います。

ピッチ円直径が重要な理由として歯車の軸間距離や、次のモジュールを決定する上で重要な役割を果たし、歯車機構を設計する上で必要な値だからです。

 

② モジュールとは
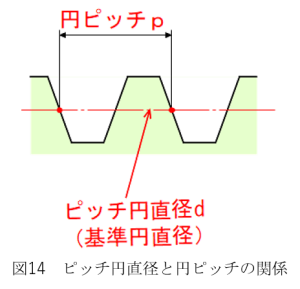
モジュールは歯車の歯の大きさを表す値
です。図14に示すようにピッチ円直径ｄを
歯車の歯数ｚで割ると以下の関係となります。

\(p=\displaystyle \frac{πd}{z}=πm\)

（ｐ：円ピッチ　ｍ：モジュール）
円ピッチは、隣り合うピッチ点とピッチ点
の間隔です。この円ピッチｐの間隔が合え
ば大きさの異なる歯車で合っても噛み合
うことができます。　
この式を整理すると以下の式となります。

\(m=\displaystyle \frac{d}{z}\) 　（\(モジュール=\displaystyle \frac{基準ピッチ円直径}{歯数}\)）

つまり、モジュールとは基準ピッチ円直径を歯数で割ったもので、歯の大きさをわかりやすく表した値です。このモジュールの値が同じ値であれば、歯車の大きさが異なっていても変わらず噛み合います。逆にモジュールの異なる歯車同士は円ピッチが合わないため絶対に噛み合いません。
なお、モジュールの値は勝手に決めているわけではなく、標準数を用いてJIS規格（JIS B1701）で規定されています。

③ バックラッシとは
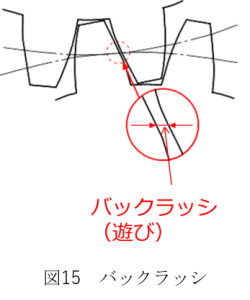バックラッシは一対の歯車をかみ合わせた時に生じる歯面間の「遊び」のことです。経験が浅いと、遊びつまり隙間があると精度が出なくなると考えてバックラッシなどない方がいいと考えがちです。
しかしながら、このバックラッシが0の状態となると噛み合う歯車の歯同士が干渉してしまい、歯車を回転させることができなくなります。
バックラッシが小さすぎると歯車の潤滑が不十分になり、歯面同士の摩耗が大きくなり、歯車の寿命が低下します。一方でバックラッシが大きすぎると、歯車同士の噛み合いが悪くなり、騒音や振動の発生原因となります。
バックラッシの目安としては歯車のサイズが500㎜以下の場合は0.1㎜程度、500㎜以上の場合は0.2㎜程度で設定します。

（3）歯車の組み合わせ

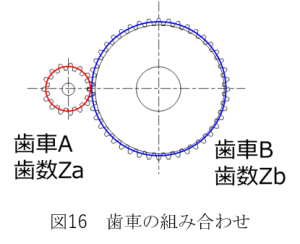
次に歯車の組み合わせについて説明します。
先に説明したようにモジュールの値が一致すれば歯車は噛み合います。
しかしながら、何でも噛み合えばよいというものでもありません。

例えば、噛み合う一対の歯車Aと歯車Bにおいて歯車Aの歯数Zaが14、歯車Bの歯数Zbが28とします。
歯数Zaと歯数Zbとの比率が1：2なので歯車Aが２回転すると歯車Bは１回転します。歯車Aおよび歯車Bの歯に1番から順に番号を振っていった場合、歯車Aの１番目の歯は歯車Bの１番目の歯と15番目の歯と噛み合います。このかみ合わせの関係は歯車Aと歯車Bが回転を続ける限り、この関係が成り立ちます。つまり、歯車Aの１番目の歯は歯車Bの１番目の歯と15番目の歯としか噛み合いません。その結果、歯車Aの１番目の歯と、歯車Bの１、15番目の歯には偏摩耗が生じます。これにより、歯車Aと歯車Bの寿命が想定以上に短くなる可能性が高くなります。

では、歯車同士の組み合わせにおいてできる限り寿命を延ばしたい場合、どうしたらいいでしょうか？
1つの方法としては、歯車Aと歯車Bのすべての歯を満遍なく噛み合わせる方法があります。具体的には、歯車Aの歯数と歯車Bの歯数の公約数が1のみとなる状態に互いの歯数を設定することです。この状態を“互いに素になる”と言います。

例えば、歯車Aの歯数Zaが14、歯車Bの歯数Zbが27とします。このように歯数を設定すると、歯車Aと歯車Bを回転させると、歯車Aが1周目の場合、歯車Aの１番目の歯は歯車Bの１番目の歯と噛み合い、歯車Aが2周目の場合、15番目の歯と噛み合います。さらに歯車Aが3周目の場合、歯車Bの2番目の歯と噛み合い、歯車Aが4周目の場合、歯車Bの16番目の歯と噛み合うという風に歯車Aの１番目の歯と噛み合う歯車Bの歯が１個ずつ後ろにずれていきます。これにより、歯車Aの１番目の歯が歯車Bの１番目の歯と噛み合うには27回転する必要があります。この間、歯車Aの１番目の歯は歯車Bの全ての歯と噛み合うことになります。これにより、歯車A、Bの特定の歯同士が偏って噛み合うことがなく、偏摩耗を抑制することができ、歯車の寿命を延ばすことができます。

4.歯車の変速

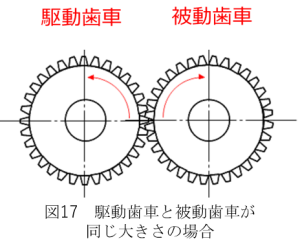次に歯車の速度について説明します。図17に示すように噛み合う歯車のうち、回転を伝える側の歯車を駆動歯車と呼び、
回転を伝えられる側の歯車を被動歯車と呼びます。駆動歯車と被動歯車の大きさが同じ場合、駆動歯車の回転速度と被動歯車の回転速度は同じになります。一方で被動歯車の回転方向は駆動歯車と逆になります。
では駆動歯車と被動歯車の大きさが異なる場合はどうでしょうか？
駆動歯車をAとし、その歯数をZ1、ピッチ円直径をｄ1、被動歯車をBとし、歯数をZ2、ピッチ円直径をd2とします。

 

ぱっと見であきらかに被動歯車Bを１回転させるのに駆動歯車Aを何回転もさせる必要があるのはわかるはずです。では、駆動歯車と被動歯車の大きさが異なる場合の回転速度を求めてみましょう。
歯車Aが回転数N1で回転している場合、歯車Bの回転数N2は次の式で表せます。
\(N_{2}=(Z_{1}/Z_{2})×N_{1}\) （式1）
逆に被動歯車Bが回転数N2で回転している場合、回転数N1は次の式で表せます。
\(N_{1}=(Z_{2}/Z_{1})×N_{2}\)（式2）
この式から以下の関係が成り立ちます。

\(\displaystyle 速度伝達比i=\frac{N_{1}}{N_{2}}=\frac{d_{2}}{d_{1}}=\frac{Z_{2}}{Z_{1}}\)（式3）

つまり、歯車間の回転速度は、歯数に依存して確実に伝達されることがわかります。
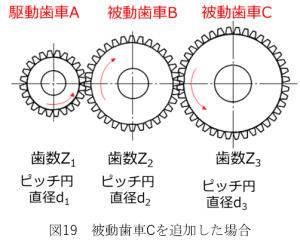
次にさらに被動歯車を増やしていった場合、歯車間の速度伝達がどうなるかを説明します。図19に被動歯車Cを追加した場合を示します。
駆動歯車Aの歯数をZ1、ピッチ円直径をd1とし、被動歯車Bの歯数をZ2、ピッチ円直径をd2とし、被動歯車Cの歯数をZ3、ピッチ円直径をd3とします。

この場合、駆動歯車A、被動歯車B、被動歯車Cの間には以下の関係が成り立ちます。

\(\displaystyle 速度伝達比i=\frac{N_{1}}{N_{3}}=\frac{N_{1}}{N_{2}}×\frac{N_{2}}{N_{3}}=\frac{d_{3}}{d_{1}}=\frac{Z_{3}}{Z_{1}}\)（式4）

式4に示すように、駆動歯車A、被動歯車B、被動歯車Cの速度伝達比の式では中間の被動歯車Bの値が消えます。つまり、速度伝達比は最初の駆動歯車と最後の被動歯車の歯数の比で決まります。したがって、被動歯車の数を増やしても、速度伝達比は最初の駆動歯車と最後の被動歯車の歯数の比で決まります。最初の駆動歯車と最後の被動歯車の間の被動歯車を遊び車と呼びます。遊び車の役割は歯車の回転方向を変えます。因みに、複数の歯車からなる歯車列では、歯車の個数が偶数の場合、最後の被動歯車の回転方向は駆動歯車と逆の方向に回転し、歯車の個数が奇数の場合、最後の被動歯車の回転方向は駆動歯車と同じ方向に回転します。

歯車には、歯車の歯数比を変えて変速する歯車減速機構というものがあり、多くの産業機械や家電製品等で使用されています。また、今回は説明しませんでしたが、歯車の速度を変えることで歯車が伝達する力も変化します。より深く歯車を知りたい場合は、ぜひ歯車について学んでみてください。

次回は機械要素の第2回としてねじについて説明します。